Subespacios complementarios
Dos subespacios vectoriales se dicen complementarios cuando forman una suma directa y su suma coincide con todo el espacio vectorial.
Definición de subespacios complementarios
Sean A y B dos subespacios del espacio vectorial V. Se dice que A y B son subespacios complementarios si se verifica que:
$$ \begin{cases} A \oplus B \\ A + B = V \end{cases} $$
La primera condición (suma directa) implica que la intersección entre los dos subespacios es trivial:
$$A \oplus B \Rightarrow A \cap B = \{ 0_v \} $$
La segunda condición establece que la suma de los subespacios A+B genera todo el espacio vectorial V:
$$ A+B = V $$
Cuando se cumplen ambas condiciones, se expresa como:
$$A \oplus B = V $$
Es imprescindible que se cumplan las dos propiedades: ni la intersección trivial ni la suma del espacio, por sí solas, son suficientes para garantizar la complementariedad.
Diferencia entre suma directa y suma de subespacios. La suma directa exige que la única intersección entre los subespacios sea el vector nulo { 0v }, mientras que la suma de subespacios es simplemente el conjunto de todas las combinaciones lineales entre sus elementos.
Ejemplos prácticos
Veamos algunos ejemplos para determinar si dos subespacios vectoriales son complementarios.
Ejemplo 1
Sea V un espacio vectorial sobre R3, y consideremos dos subespacios A y B definidos como:
$$ A = \{ (x,y,z) \in R^3 \mid x=0,\ y=0 \} $$
$$ B = \{ (x,y,z) \in R^3 \mid z=0 \} $$
El subespacio A corresponde al eje Z (azul) en el espacio tridimensional.
El subespacio B, por su parte, es el plano XY (rojo) en R3 con z=0.
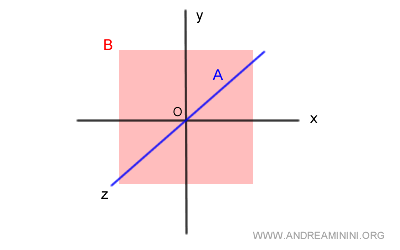
La intersección A ∩ B contiene únicamente el vector nulo 0v:
$$ A \cap B = \{0_v\} $$
Por tanto, A y B están en suma directa:
$$ A \oplus B $$
Se cumple así la primera condición de complementariedad.
Verifiquemos ahora si su suma genera todo el espacio V:
$$ A + B = V $$
La suma desplaza el plano B a lo largo del eje Z, llenando todo el espacio tridimensional.
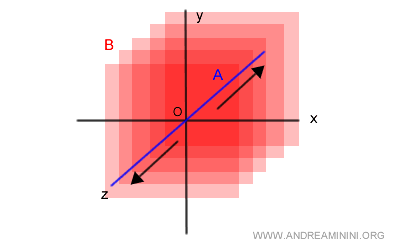
Por tanto, se cumple también la segunda condición:
Los subespacios A y B son complementarios.
Ejemplo 2
Sea V = R3, y definamos los subespacios:
$$ A = \{ (x,y,z) \in R^3 \mid x=0,\ y=0 \} $$
$$ B = \{ (x,y,z) \in R^3 \mid z=0,\ y=0 \} $$
El subespacio A es nuevamente el eje Z (azul), mientras que B es el eje X (rojo).
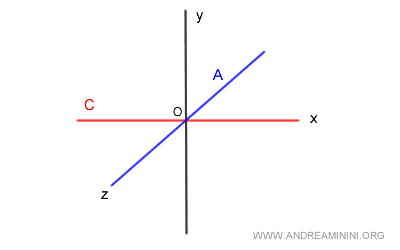
La intersección A ∩ B es trivial:
$$ A \cap B = \{0_v\} $$
Así, A y B están en suma directa:
$$ A \oplus B $$
Pero su suma no cubre todo R3:
$$ A + B = \{ (x,0,z) \in R^3 \} $$
Es decir, corresponde al plano XZ en R2, no al espacio completo R3.
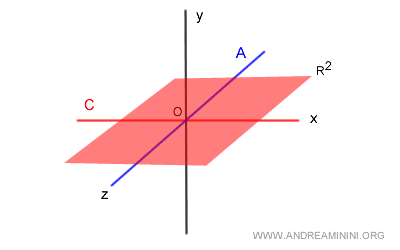
Por tanto, aunque estén en suma directa, los subespacios A y B no son complementarios.
Ejemplo 3
En R3, consideramos los siguientes subespacios:
$$ A = \{ (x,y,z) \in R^3 \mid x=0,\ y=0 \} $$
$$ C = \{ (x,y,z) \in R^3 \mid y=0 \} $$
A es el eje Z (azul), mientras que C es el plano XZ (rojo), con y=0.
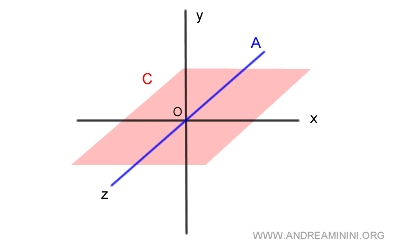
Calculamos su intersección:
$$ A \cap C = \{ (0,0,z) \in R^3 \} $$
La intersección no es trivial: contiene todos los puntos del eje Z.
Por tanto, A y C no están en suma directa.
En consecuencia, A y C no son subespacios complementarios.
No es necesario verificar si su suma genera V.
Y así sucesivamente.