Suma directa de subespacios vectoriales
La suma de dos subespacios $A$ y $B$ se denomina suma directa si su intersección contiene únicamente el vector nulo.
Dado un espacio vectorial $V$ sobre un cuerpo $K$, y dos subespacios $A$ y $B$ de $V$, se dice que su suma es directa si $$ A \cap B = \{ \vec{0} \} $$ En tal caso, se denota como: $$ A \oplus B $$
La notación $\oplus$ (suma con símbolo de círculo) indica explícitamente que se trata de una suma directa, es decir, con intersección trivial.
Ejemplos prácticos
A continuación se presentan dos ejemplos que permiten verificar, mediante el cálculo explícito, si dos subespacios están en suma directa o no.
Ejemplo 1
En el espacio vectorial $V = \mathbb{R}^3$, consideremos los subespacios:
$$ A = \{ (x, y, z) \in \mathbb{R}^3 \mid x = 0, \ y = 0 \} $$
$$ B = \{ (x, y, z) \in \mathbb{R}^3 \mid z = 0 \} $$
El subespacio $A$ corresponde al eje $z$ (en azul), mientras que $B$ representa el plano $xy$ definido por $z = 0$ (en rojo).
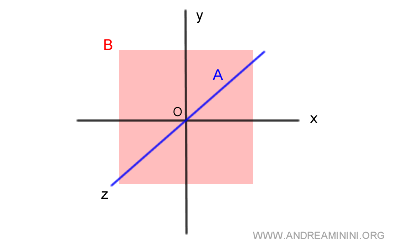
Verificamos si su intersección contiene únicamente el vector nulo:
$$ A \cap B = \{ \vec{0} \} $$
Lo cual se cumple, ya que el único vector que pertenece simultáneamente a ambos subespacios es el vector nulo (el origen $O$).
Por lo tanto, los subespacios $A$ y $B$ están en suma directa:
$$ A \oplus B $$
Ejemplo 2
En el mismo espacio $V = \mathbb{R}^3$, consideremos ahora los subespacios:
$$ A = \{ (x, y, z) \in \mathbb{R}^3 \mid x = 0, \ y = 0 \} $$
$$ C = \{ (x, y, z) \in \mathbb{R}^3 \mid y = 0 \} $$
El subespacio $A$ representa, como antes, el eje $z$ (en azul), mientras que $C$ es el plano $xz$ definido por $y = 0$ (en rojo).
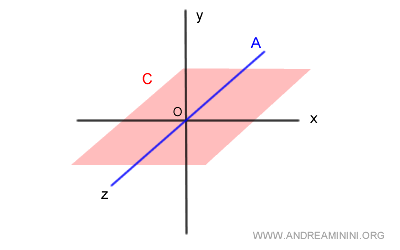
Analizamos ahora su intersección:
$$ A \cap C = \text{eje } z \ne \{ \vec{0} \} $$
En efecto, $A \cap C$ contiene todos los vectores del eje $z$, es decir, una infinidad de elementos distintos de $\vec{0}$.
Por tanto, $A$ y $C$ no están en suma directa.
Y así sucesivamente.