Suma de subespacios vectoriales
Sea V un espacio vectorial sobre un cuerpo K, y sean A y B dos subespacios de V. La suma A + B se define como el conjunto de todas las sumas de un vector de A con uno de B: $$ A + B := \{ \vec{a} + \vec{b} \mid \vec{a} \in A, \ \vec{b} \in B \} $$ Este conjunto forma un subespacio vectorial que contiene, en particular, la unión de ambos subespacios: $$ A \cup B \subset A + B $$ Además, A + B es el subespacio vectorial más pequeño de V que contiene dicha unión.
La suma A + B es, por tanto, un subespacio de V, y se denomina subespacio suma.
$$ A + B \subseteq V $$
Al ser V un espacio vectorial, hereda todas las propiedades definitorias de los espacios vectoriales.
De hecho, A y B están contenidos en su suma:
$$ A \subset A + B \qquad B \subset A + B $$
Y, como ya se ha dicho, A + B es el menor subespacio de V que contiene simultáneamente A y B.
Nota. La unión A ∪ B no es, en general, un subespacio vectorial, ya que la unión de subespacios no está cerrada bajo suma de vectores.
Demostración
A + B es un subespacio vectorial
Queremos demostrar que la suma de dos subespacios vectoriales sigue siendo un subespacio.
Dado que A y B son subespacios, ambos contienen el vector nulo. Por tanto, su suma también:
$$ \vec{0} = \vec{0} + \vec{0} \in A + B $$
Comprobamos ahora las dos propiedades características de un subespacio:
1) Cerradura bajo la suma
Sean $\vec{u}, \vec{w} \in A + B$ dos vectores cualesquiera. Entonces existen $\vec{a}_1, \vec{a}_2 \in A$ y $\vec{b}_1, \vec{b}_2 \in B$ tales que:
$$ \vec{u} = \vec{a}_1 + \vec{b}_1 \qquad \vec{w} = \vec{a}_2 + \vec{b}_2 $$
La suma de $\vec{u}$ y $\vec{w}$ es:
$$ \vec{u} + \vec{w} = (\vec{a}_1 + \vec{b}_1) + (\vec{a}_2 + \vec{b}_2) $$
Aplicando la propiedad asociativa:
$$ \vec{u} + \vec{w} = (\vec{a}_1 + \vec{a}_2) + (\vec{b}_1 + \vec{b}_2) $$
Como A y B son subespacios, sus sumas internas también pertenecen a ellos:
$$ \vec{a}_1 + \vec{a}_2 \in A \qquad \vec{b}_1 + \vec{b}_2 \in B $$
Luego:
$$ \vec{u} + \vec{w} \in A + B $$
Se verifica así la cerradura bajo la suma.
2) Cerradura bajo la multiplicación escalar
Sea $k \in K$ un escalar arbitrario, y sea $\vec{u} = \vec{a} + \vec{b} \in A + B$ con $\vec{a} \in A$, $\vec{b} \in B$.
Entonces:
$$ k \vec{u} = k (\vec{a} + \vec{b}) = k \vec{a} + k \vec{b} $$
Dado que A y B son subespacios, se cumple:
$$ k \vec{a} \in A \qquad k \vec{b} \in B $$
Por lo tanto:
$$ k \vec{u} \in A + B $$
Se satisface también la cerradura bajo multiplicación escalar.
Como A + B contiene el vector nulo y es cerrado bajo suma y multiplicación por escalares, concluimos que es un subespacio vectorial.
La suma A + B contiene la unión A ∪ B
Ahora queremos mostrar que la suma A + B contiene la unión A ∪ B.
Para todo vector $\vec{a} \in A$, se puede escribir:
$$ \vec{a} = \vec{a} + \vec{0} \in A + B $$
Y para todo $\vec{b} \in B$:
$$ \vec{b} = \vec{0} + \vec{b} \in A + B $$
En consecuencia:
$$ A \subset A + B \qquad B \subset A + B $$
y por tanto:
$$ A \cup B \subset A + B $$
La suma A + B incluye todos los vectores de A y de B, es decir, contiene la unión de los dos subespacios.
Un ejemplo práctico
Consideremos el espacio vectorial $V = \mathbb{R}^3$.
$$ V = \mathbb{R}^3 $$
Sean ahora dos subespacios vectoriales definidos como:
$$ A = \{ \vec{a} \in \mathbb{R}^3 \mid \vec{a} \text{ sobre el eje } x \} $$
$$ B = \{ \vec{b} \in \mathbb{R}^3 \mid \vec{b} \text{ sobre el eje } y \} $$
El subespacio A está formado por todos los vectores alineados con el eje X.
El subespacio B está formado por todos los vectores alineados con el eje Y.
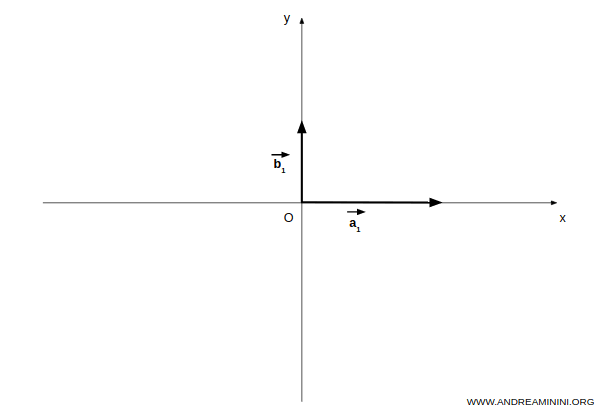
Consideremos ahora la suma de estos subespacios, denotada $A + B$:
$$ A + B $$
La suma $A + B$ contiene todos los vectores de A y de B, así como sus combinaciones lineales.
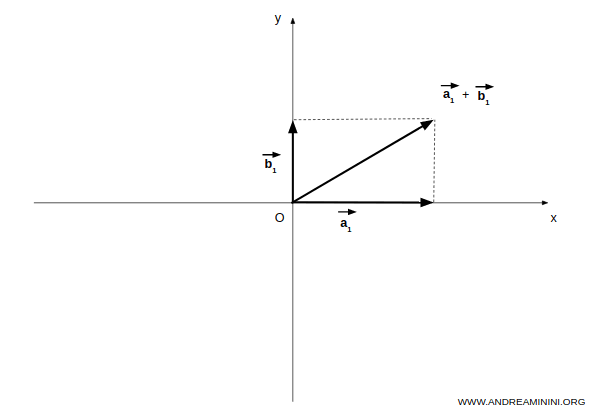
Como subespacio, $A + B$ está cerrado bajo la suma y la multiplicación escalar, y por tanto contiene todo el plano XY generado por los vectores de A y B.
El subespacio mínimo que contiene A y B
La suma $A + B$ es el subespacio vectorial más pequeño de $V$ que contiene la unión $A \cup B$.
Demostración
Sea $L$ un subespacio de $V$ tal que contiene todos los elementos de $A$ y $B$, es decir:
$$ A \cup B \subseteq L $$
Entonces, por definición de inclusión:
$$ \forall \vec{a} \in A, \quad \vec{a} \in L $$
$$ \forall \vec{b} \in B, \quad \vec{b} \in L $$
Dado que $L$ es un subespacio, debe ser cerrado bajo la suma de vectores, lo que implica:
$$ \{ \vec{a} + \vec{b} \mid \vec{a} \in A, \ \vec{b} \in B \} \subseteq L $$
Es decir:
$$ A + B \subseteq L $$
Por tanto, cualquier subespacio que contenga a $A$ y a $B$ debe contener necesariamente su suma $A + B$.
De ello se sigue que $A + B$ es el subespacio más pequeño que contiene a $A \cup B$.
Nota. El subespacio $A + B$ está contenido en todo subespacio que contenga simultáneamente a $A$ y $B$. Por consiguiente, es el menor con esta propiedad. Cualquier subconjunto $Z$ tal que $$ A, B \subset Z \subset A + B $$ no puede ser un subespacio vectorial, ya que no estaría cerrado bajo suma. Por ejemplo, si $\vec{a} \in A$ y $\vec{b} \in B$, entonces $\vec{a} + \vec{b} \in A + B$, pero no necesariamente $\vec{a} + \vec{b} \in Z$. Por ello, $A + B$ es el único subespacio mínimo que contiene a $A$ y $B$.
Y así sucesivamente.