Subespacio vectorial
¿Qué es un subespacio vectorial?
Un subespacio vectorial es un subconjunto de un espacio vectorial que cumple todas las propiedades que definen a los espacios vectoriales.
Definición de subespacio vectorial
- Sea V un espacio vectorial sobre un cuerpo K. Un subconjunto W es un subespacio vectorial de V $$ W \subseteq V $$ si satisface las siguientes condiciones:
- Para cualesquiera vectores w1 y w2 en W, su suma también pertenece a W. $$ \forall \ \vec{w}_1, \vec{w}_2 \in W \ \Rightarrow \ \vec{w}_1 + \vec{w}_2 \in W $$
- Para todo escalar λ en K y todo vector w en W, el producto λw también pertenece a W. $$ \forall \ \lambda \in K, \ \forall \ \vec{w} \in W \ \Rightarrow \ \lambda \cdot \vec{w} \in W $$
Dicho de otro modo, un subespacio vectorial es un subconjunto cerrado bajo las operaciones de suma y multiplicación escalar.
Todo subespacio vectorial es, por sí mismo, un espacio vectorial.
Por tanto, todas las propiedades de los espacios vectoriales también se cumplen en cualquier subespacio.
Nota. Esto es fundamental: no todo subconjunto de un espacio vectorial es un subespacio. Para comprobarlo, es necesario verificar que satisfaga los axiomas correspondientes.
¿Cómo saber si un subconjunto es un subespacio?
Una de las primeras comprobaciones consiste en verificar si el subconjunto contiene el vector nulo.
¿Por qué es esto importante?
La existencia del vector nulo es una de las propiedades esenciales de todo espacio vectorial.
Como los subespacios son espacios vectoriales en sí mismos, deben contener necesariamente el vector nulo.
Si un subconjunto no contiene el vector nulo, entonces no puede ser un subespacio vectorial.
Una vez confirmada la presencia del vector nulo, hay que comprobar que se cumplan las dos propiedades clave: clausura bajo la suma y bajo la multiplicación escalar.
Un subconjunto es un subespacio vectorial si cumple ambas propiedades fundamentales:
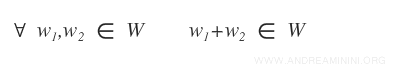
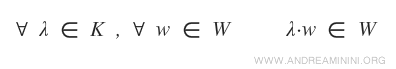
En la práctica, esto implica verificar que la suma de dos elementos de W y la multiplicación de un vector de W por un escalar siguen produciendo elementos que pertenecen a W.
Si ambas condiciones se cumplen, entonces W es un subespacio vectorial. De lo contrario, no lo es.
Ejemplo práctico
Ejemplo 1
En este ejemplo sencillo, determinamos si un subconjunto W constituye un subespacio vectorial.

Ejemplo 2
En el segundo ejemplo, analizamos otro subconjunto.
En este caso, la ecuación resulta igual a uno, lo que lleva a una conclusión completamente distinta.

Más ejercicios resueltos
Identificación gráfica de subespacios vectoriales
También es posible analizar si un subconjunto cumple las propiedades de subespacio observando su representación gráfica en el plano cartesiano.
Si el subconjunto W contiene el vector nulo (0,0), su gráfica pasará por el origen O.
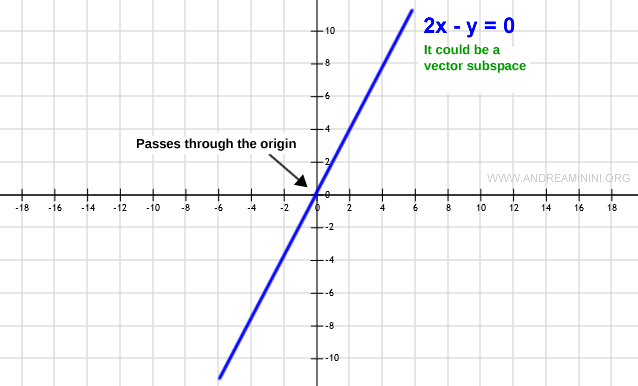
Nota. Esta condición es necesaria, pero no suficiente. Que la gráfica pase por el origen no garantiza por sí solo que se trate de un subespacio. Es sólo el primer paso.
Si, por el contrario, la gráfica no pasa por el origen, entonces el subconjunto no contiene el vector nulo.
En ese caso, W no es un subespacio vectorial.
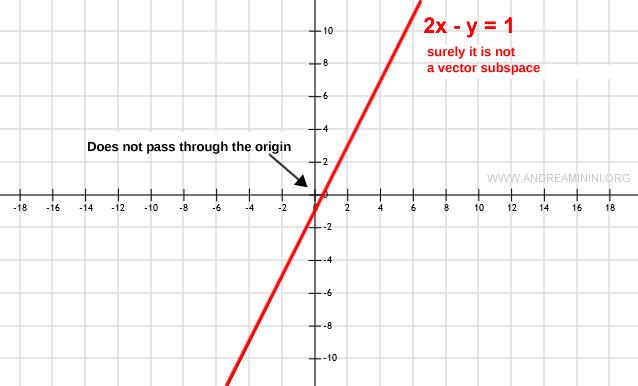
Nota. Si la gráfica no pasa por el origen, ya se puede descartar el subconjunto como subespacio sin necesidad de comprobar otras propiedades.
En caso de que la línea sí pase por el origen, será necesario comprobar si el subconjunto cumple las dos condiciones fundamentales.
Es un subespacio si...
El subconjunto W es un subespacio si la suma de cualesquiera dos vectores de W produce otro vector que también pertenece a W (es decir, que permanece sobre la recta).
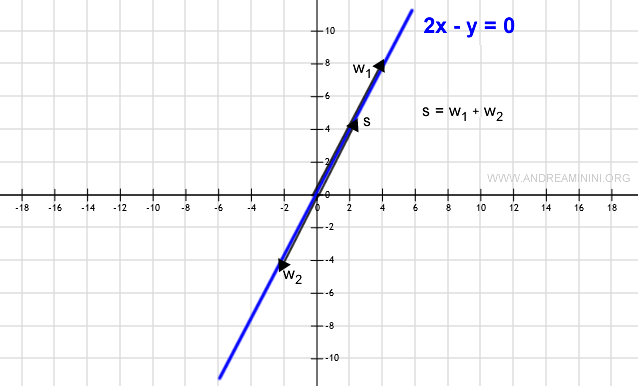
Además, al multiplicar cualquier vector w por un escalar, el resultado también debe permanecer sobre la recta (dentro de W).
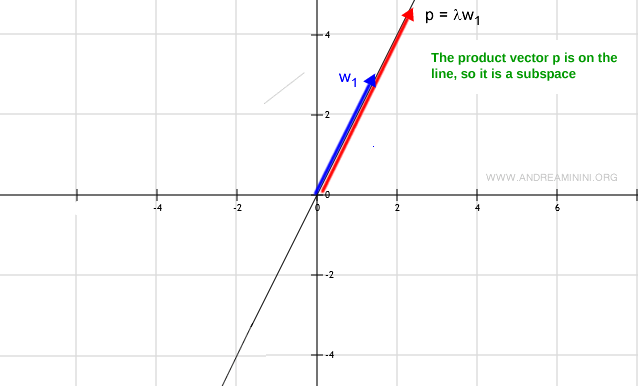
No es un subespacio si...
W no es un subespacio si la suma w1 + w2 produce un vector que no pertenece al subconjunto (por ejemplo, que no está sobre la recta).
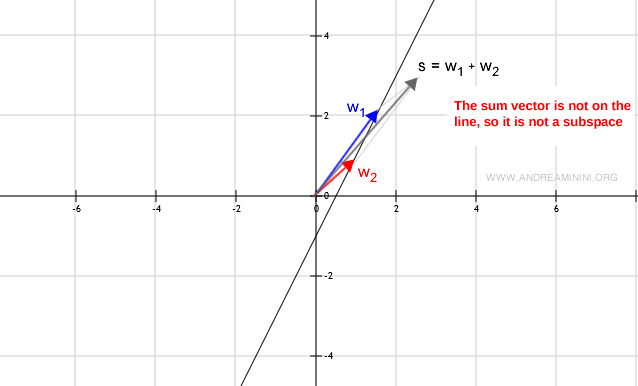
O si la multiplicación escalar λw produce un vector fuera de la recta, lo cual también viola la condición de clausura.
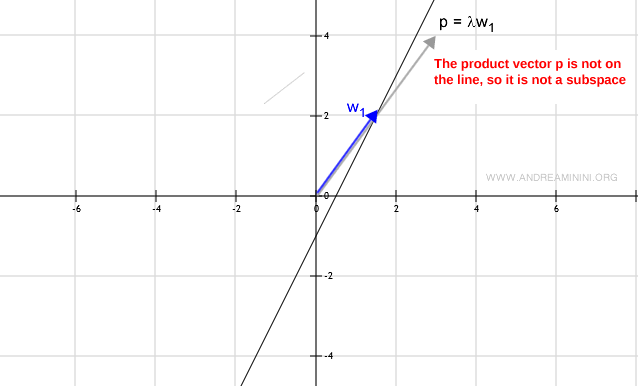
En resumen, el análisis gráfico también puede ser una herramienta útil para identificar subespacios vectoriales.
Subespacios vectoriales y combinaciones lineales
Un subconjunto W de un espacio vectorial V es un subespacio si toda combinación lineal de sus elementos (con escalares de K) también pertenece a W.

Esta formulación encapsula las dos propiedades fundamentales del subespacio: la clausura bajo la suma y la multiplicación escalar.