Ejercicio 3: Subespacio vectorial

Sea $V = \mathbb{R}^2$ y consideremos el subconjunto: $$ W = \{ (x, y) \in \mathbb{R}^2 \mid x^2 - y = 0 \} $$ Se nos pide determinar si $W$ es un subespacio vectorial de $V$.

Para que $W$ califique como subespacio, debe cumplir todos los axiomas de un espacio vectorial: debe contener el vector nulo, y ser cerrado tanto bajo la suma vectorial como bajo la multiplicación por escalares.

1) Verificación del vector nulo

Sea $\vec{w} = \begin{pmatrix} x \\ y \end{pmatrix}$ un vector genérico en $W$. Por definición:

$$ \vec{w} \in W \quad \Leftrightarrow \quad x^2 - y = 0 $$

Comprobamos si el vector nulo $\begin{pmatrix} 0 \\ 0 \end{pmatrix}$ pertenece a $W$:

$$ 0^2 - 0 = 0 $$

La condición se satisface, por lo tanto el vector nulo pertenece a $W$.

Nota. Verificar la presencia del vector nulo es un paso preliminar esencial. Si no está incluido en el conjunto, este no puede ser un subespacio vectorial, y no es necesario seguir evaluando otras propiedades.

2) Cerradura bajo la suma de vectores

Examinemos ahora si $W$ es cerrado bajo la suma. Tomemos dos vectores arbitrarios en $W$:

$$ \vec{w}_1 = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix}, \quad \text{con } x_1^2 - y_1 = 0 $$

$$ \vec{w}_2 = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix}, \quad \text{con } x_2^2 - y_2 = 0 $$

Sumamos ambos vectores:

$$ \vec{w}_1 + \vec{w}_2 = \begin{pmatrix} x_1 + x_2 \\ y_1 + y_2 \end{pmatrix} $$

Verificamos si el vector resultante también satisface la condición $x^2 - y = 0$:

$$ (x_1 + x_2)^2 - (y_1 + y_2) = x_1^2 + 2x_1x_2 + x_2^2 - y_1 - y_2 $$

Reagrupamos términos:

$$ = (x_1^2 - y_1) + (x_2^2 - y_2) + 2x_1x_2 $$

Dado que $x_1^2 - y_1 = 0$ y $x_2^2 - y_2 = 0$, la expresión se reduce a:

$$ 0 + 0 + 2x_1x_2 = 2x_1x_2 $$

Esta expresión es igual a cero únicamente si $x_1 = 0$ o $x_2 = 0$, pero no en general.

Por lo tanto, la suma $\vec{w}_1 + \vec{w}_2$ no pertenece necesariamente a $W$:

$$ \vec{w}_1 + \vec{w}_2 \notin W $$

Esto implica que $W$ no es cerrado bajo la suma vectorial, lo que infringe uno de los requisitos fundamentales para ser subespacio.

En consecuencia, $W$ no es un subespacio vectorial de $\mathbb{R}^2$.

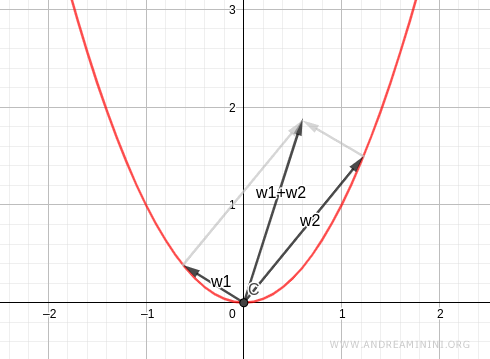
Nota. Desde un punto de vista geométrico, la ecuación $x^2 - y = 0$ representa una parábola, no una recta. La suma de dos vectores que pertenecen a una parábola, salvo casos particulares, no se encuentra sobre ella.

Y así sucesivamente.