Generadores de un espacio vectorial

Un sistema generador es un conjunto de vectores $S = \{ v_1, \dots, v_m \} \subset V$ tal que todo vector $v_i \in V$ puede escribirse como una combinación lineal de los vectores de $S$, con coeficientes escalares $a_1, \dots, a_m \in \mathbb{R}$: $$ \vec{v}_i = a_1 \vec{v}_1 + \cdots + a_m \vec{v}_m \quad \forall \ v_i \in V $$

Es decir, las combinaciones lineales de los vectores de $S = \{ v_1, \dots, v_m \}$ generan todos los vectores del espacio $V$.

Por esta razón, los vectores de $S$ se denominan generadores.

Así, dado un conjunto $S$ de vectores en el espacio vectorial $V$:

$$ S = \{ v_1, v_2, \dots, v_n \} $$

El subespacio lineal más pequeño que contiene a $S$ coincide con todo el espacio $V$:

$$ L(S) = V $$

El número de generadores puede ser finito o infinito, siempre que no exceda la cantidad necesaria para describir completamente el espacio:

$$ m \le i $$

En estas notas, $S$ denota el conjunto generador y $L(S)$ el subespacio que genera.

¿Para qué sirve un sistema generador?

Un espacio vectorial $V$ puede contener infinitos vectores, pero no es necesario enumerarlos todos para caracterizarlo.

De hecho, todo vector $v \in V$ puede expresarse como combinación lineal de un subconjunto adecuado de vectores del propio espacio.

Ejemplo

$$ v_4 = a_1 v_1 + a_2 v_2 + a_3 v_3 $$ $$ v_5 = a_1 v_1 + a_2 v_2 + a_3 v_3 $$ $$ v_6 = a_1 v_1 + a_2 v_2 + a_3 v_3 $$ $$ \vdots $$

Es suficiente seleccionar un subconjunto finito (o infinito) de vectores generadores:

$$ L = \{ v_1, v_2, v_3 \} $$

Combinando linealmente los vectores de $S$ con escalares $\alpha_m$, podemos obtener cualquier vector de $V$:

$$ \forall \ v \in V \quad v = a_1 v_1 + a_2 v_2 + a_3 v_3 $$

Ejemplo de sistema generador

El espacio vectorial completo $V = \mathbb{R}^2$ puede generarse mediante solo dos vectores:

$$ v_1 = (1, 0) \qquad v_2 = (0, 1) $$

En el plano cartesiano $\mathbb{R}^2$, estos vectores se representan así:

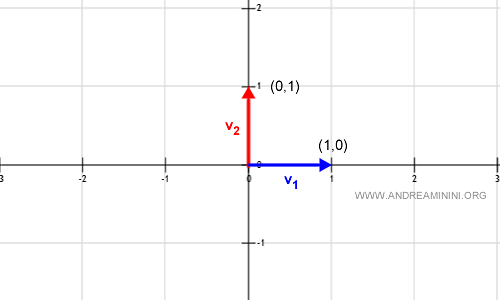
Para verificar que $v_1$ y $v_2$ generan $\mathbb{R}^2$, consideramos la siguiente combinación lineal con escalares reales $a_1$ y $a_2$:

$$ v = a_1 v_1 + a_2 v_2 \quad \text{con} \quad a_1 = 1, \ a_2 = 1 $$

$$ v = (1, 0) + (0, 1) = (1, 1) $$

Este nuevo vector, con coordenadas (1,1), pertenece a $\mathbb{R}^2$:

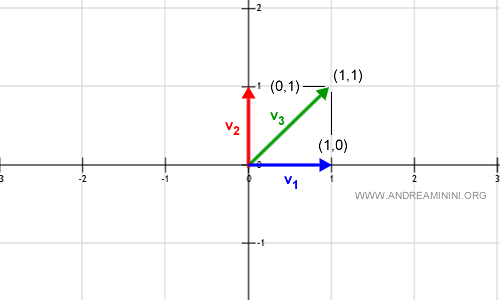
Si ahora variamos $a_2$ a 2:

$$ v = 1 \cdot (1, 0) + 2 \cdot (0, 1) = (1, 2) $$

Obtenemos otro vector de $\mathbb{R}^2$ con coordenadas (1,2):

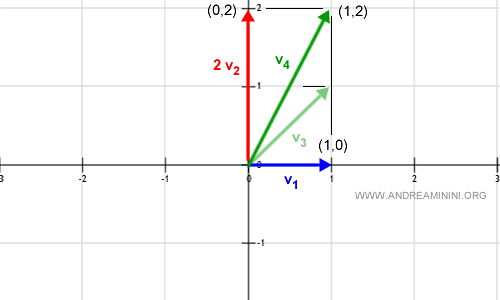
Al variar los coeficientes $a_1$ y $a_2$, podemos generar cualquier vector de $\mathbb{R}^2$. Por tanto:

$$ L_{\mathbb{R}} = \{ v_1, v_2 \} = \mathbb{R}^2 $$

Nota. Un solo vector, como $v_1$, no genera $\mathbb{R}^2$ porque solo permite obtener vectores sobre el eje $x$. Análogamente, $v_2$ genera únicamente el eje $y$. Por separado, cada uno genera un subespacio unidimensional.

Ejemplo 2

Un sistema generador también puede estar formado por un único vector, siempre que no sea nulo.

Sea $V$ un espacio vectorial sobre el cuerpo $K = \mathbb{R}$, y $\vec{v} \in V$ un vector no nulo:

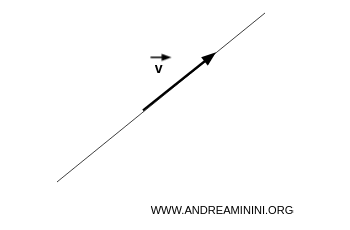
El conjunto generado por $v$ está dado por:

$$ L(v) = \{ k \cdot \vec{v} \mid k \in K \} $$

Los vectores generados tienen todos la misma dirección, y forman una recta:

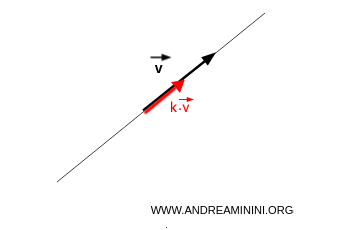
Lo que cambia es la magnitud y el sentido de cada vector.

Nota. El vector generador no debe ser nulo, ya que cualquier escalar multiplicado por el vector nulo sigue siendo el vector nulo.

Ejemplo 3

En general, dos vectores no nulos generan un subespacio que depende de si son o no linealmente independientes:

$$ \vec{v}_1 \ne \vec{0} \qquad \vec{v}_2 \ne \vec{0} $$

• Si los vectores son paralelos $$ \vec{v}_1 = k \cdot \vec{v}_2 $$ El subespacio generado $L(v_1, v_2)$ corresponde a una recta:
  
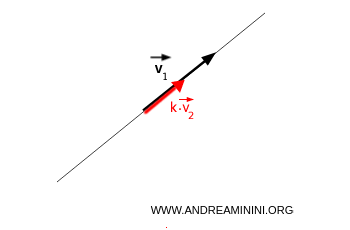
• Si los vectores no son paralelos $$ \vec{v}_1 \ne k \cdot \vec{v}_2 $$ El subespacio generado por $v_1$ y $v_2$ es el plano que contiene a ambos:
  

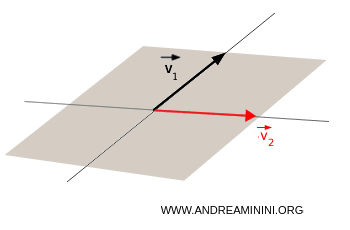
Cómo determinar si un conjunto de vectores es generador

Para comprobar si un conjunto de vectores genera un espacio vectorial $V$, basta analizar si toda combinación lineal de sus elementos puede representar cualquier vector de $V$. Para ello, se plantea el sistema de ecuaciones correspondiente a su combinación lineal.

Ejemplo práctico

Consideremos los vectores $v_1 = (1,1)$ y $v_2 = (2,1)$ en el espacio vectorial $V = \mathbb{R}^2$.

Queremos determinar si estos vectores generan todo el plano $\mathbb{R}^2$.

Formamos la combinación lineal:

$$ a_1 v_1 + a_2 v_2 = a_1 (1,1) + a_2 (2,1) = (a_1 + 2a_2,\ a_1 + a_2) $$

Esto debe igualarse a un vector genérico $(x, y) \in \mathbb{R}^2$, lo que lleva al sistema:

$$ \begin{cases} a_1 + 2a_2 = x \\ a_1 + a_2 = y \end{cases} $$

Si este sistema tiene solución para todo $(x, y)$, entonces los vectores $v_1$ y $v_2$ generan $\mathbb{R}^2$.

Nota. Según el teorema de Rouché-Capelli, un sistema lineal tiene solución si el rango de la matriz de coeficientes coincide con el de la matriz ampliada. En tal caso, el sistema es compatible (determinado o indeterminado).

En este caso, el sistema siempre tiene solución. Por tanto, $v_1$ y $v_2$ generan $\mathbb{R}^2$.

Verificación algebraica

Resolviendo el sistema:

$$ a_1 = y - a_2 \Rightarrow x = a_1 + 2a_2 = y - a_2 + 2a_2 = y + a_2 \Rightarrow a_2 = x - y $$

Luego:

$$ a_1 = y - (x - y) = 2y - x $$

Para cualquier par $(x, y)$, existen $a_1$ y $a_2$ tales que $a_1 v_1 + a_2 v_2 = (x, y)$, lo que confirma que $\{v_1, v_2\}$ es un conjunto generador de $\mathbb{R}^2$.

Diferencia entre span lineal y conjunto generador

El span lineal de un conjunto $S_p = \{ v_1, v_2, \dots, v_m \}$ es el conjunto de todas las combinaciones lineales posibles de sus vectores:

$$ L(S_p) = \left\{ a_1 v_1 + \cdots + a_m v_m \mid a_i \in \mathbb{R} \right\} $$

Este conjunto es siempre un subespacio de $V$:

$$ L(S_p) \subseteq V $$

Pero no necesariamente abarca todo $V$:

$$ L(S_p) \ne V $$

Nota. Los vectores de $S_p$ generan únicamente el subespacio $L(S_p)$. Solo si $L(S_p) = V$, decimos que $S_p$ es un conjunto generador de $V$.

Por tanto, todo conjunto generador define un span, pero no todo span define un conjunto generador completo del espacio:

$$ L(S_p) \ne L(S) = V $$

Cómo reducir un conjunto generador

Un conjunto $\{v_1, \dots, v_m\}$ puede ser generador de $V$, pero no necesariamente es el más pequeño posible. Puede contener vectores redundantes que no aportan nueva dirección.

Por ejemplo, si se añade un vector $v_{m+1}$ tal que $a_{m+1} = 0$ en todas las combinaciones, sigue siendo un sistema generador:

$$ v = a_1 v_1 + \cdots + a_m v_m + 0 \cdot v_{m+1} $$

Ejemplo

¿Cómo se reduce un conjunto generador?

Se deben eliminar los vectores linealmente dependientes, es decir, aquellos que pueden expresarse como combinación lineal de los demás.

Demostración

Supongamos que $v_m$ depende linealmente de $v_1, \dots, v_{m-1}$:

$$ v_m = \beta_1 v_1 + \cdots + \beta_{m-1} v_{m-1} $$

Entonces, cualquier combinación del tipo:

$$ v = a_1 v_1 + \cdots + a_m v_m $$

puede reescribirse como:

$$ v = a_1 v_1 + \cdots + a_m (\beta_1 v_1 + \cdots + \beta_{m-1} v_{m-1}) $$

$$ = \gamma_1 v_1 + \cdots + \gamma_{m-1} v_{m-1} $$

donde los coeficientes $\gamma_i = a_i + a_m \beta_i$ siguen perteneciendo a $\mathbb{R}$.

Por tanto, $\{v_1, \dots, v_{m-1}\}$ también es generador de $V$.

Ejemplo

Diferencia entre conjunto generador y base

Un conjunto generador es una base del espacio vectorial $V$ si, además, sus vectores son linealmente independientes:

$$ S = \{ v_1, v_2, \dots, v_n \} $$

Una base también se denomina sistema generador libre.

En este caso, cada vector de $V$ admite una única combinación lineal de los vectores de $S$:

$$ \vec{v} = a_1 v_1 + \cdots + a_n v_n \quad \text{únicamente} $$

Nota. Si los vectores del sistema generador son linealmente dependientes, entonces cada vector de $V$ puede expresarse de múltiples formas distintas, y el conjunto no es una base.