Dependencia e independencia lineal de vectores

Dados m vectores v₁, v₂, ..., v_m en un espacio vectorial V sobre un cuerpo K, estos vectores son linealmente independientes si la única combinación lineal que resulta en el vector nulo es la combinación trivial. $$ a_1 \cdot \vec{v}_1 + a_2 \cdot \vec{v}_2 + \ ... \ + \alpha_m \cdot \vec{v}_m = \vec{0} $$ En cambio, si existen soluciones no triviales, los vectores son linealmente dependientes.

Se dice que una combinación lineal de vectores es trivial cuando todos los coeficientes escalares son cero.

$$ a_1 = a_2 = \ ... = \ a_m = 0 $$

Si al menos uno de los coeficientes es distinto de cero, la combinación lineal es no trivial.

Vectores linealmente independientes

En un espacio vectorial V sobre un cuerpo K, los vectores v₁,...,v_m ∈ V son linealmente independientes si ninguna combinación lineal da como resultado el vector nulo, salvo la combinación trivial. $$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_m \cdot \vec{v}_m = \vec{0} \ \ \ \ \ \ \alpha \in K $$

¿Qué es una combinación lineal trivial?

Es una combinación lineal en la que todos los coeficientes son cero: { a₁=0, ..., a_m=0 }.

¿Por qué se excluye la combinación lineal trivial?

Porque cualquier combinación de vectores con coeficientes nulos produce inevitablemente un vector nulo.

$$ 0 \cdot v_1 + ... + 0 \cdot v_m = 0 $$

Por tanto, la existencia de la solución trivial no permite determinar si los vectores son dependientes o independientes.

Vectores linealmente dependientes

En un espacio vectorial V sobre el cuerpo K, los vectores v₁,...,v_m ∈ V son linealmente dependientes si existe al menos una combinación lineal, distinta de la trivial, que da como resultado el vector nulo. $$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_m \cdot \vec{v}_m = \vec{0} \ \ \ \ \ \ \alpha \in K $$

Se excluye la solución trivial, ya que no permite distinguir entre dependencia e independencia lineal.

En este caso, al menos uno de los coeficientes escalares es distinto de cero.

De aquí se deduce el siguiente teorema:

Los vectores v₁,...,v_m son linealmente dependientes si al menos uno de ellos (por ejemplo, v₁) puede expresarse como combinación lineal de los demás.

$$ v_1 = \beta_2 \cdot v_2 + ... + \beta_m \cdot v_m $$ $$ con \: \: \beta_2, ..., \beta_m \in R $$

El teorema no indica cuál de los vectores puede escribirse como combinación de los demás; simplemente afirma que existe al menos uno en tal situación si los vectores son dependientes.

Este vector podría ser cualquiera de los v₁,...,v_m, no necesariamente v₁.

Interpretación geométrica

En el espacio R², dos vectores son linealmente dependientes si son paralelos o coinciden, es decir, si pertenecen a la misma recta y tienen la misma dirección.

En el espacio R³, tres vectores son linealmente dependientes si están contenidos en un mismo plano.

Nota. Estas consideraciones geométricas solo son aplicables a espacios vectoriales de dimensión R² o R³. No pueden generalizarse a espacios de dimensión superior como R⁴, R⁵, etc.

Un ejemplo práctico

Ejemplo 1

Consideremos dos vectores en el espacio vectorial V = R², definido sobre el cuerpo de los números reales K = R:

$$ \vec{v}_1 = \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$

$$ \vec{v}_2 = \begin{pmatrix} 2 \\ 5 \end{pmatrix} $$

Planteamos la siguiente combinación lineal:

$$ a_1 \cdot \vec{v}_1 + a_2 \cdot \vec{v}_2 = \vec{0} $$

$$ a_1 \cdot \begin{pmatrix} 3 \\ 1 \end{pmatrix} + a_2 \cdot \begin{pmatrix} 2 \\ 5 \end{pmatrix} = \vec{0} $$

El vector nulo es el vector cuyas dos componentes son cero:

$$ \begin{pmatrix} 3a_1 \\ a_1 \end{pmatrix} + \begin{pmatrix} 2a_2 \\ 5a_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

Reescribimos esta ecuación vectorial como un sistema de ecuaciones:

$$ \begin{cases} 3a_1 + 2a_2 = 0 \\ \\ a_1 + 5a_2 = 0 \end{cases} $$

Resolvemos el sistema aplicando el método de sustitución: despejamos a₁ en la segunda ecuación:

$$ \begin{cases} 3a_1 + 2a_2 = 0 \\ \\ a_1 = -5a_2 \end{cases} $$

Nota. Cualquier otro método de resolución es igualmente válido; por ejemplo, la regla de Cramer.

A continuación, sustituimos a₁ en la primera ecuación y determinamos el valor de a₂:

$$ \begin{cases} 3(-5a_2) + 2a_2 = 0 \\ \\ a_1 = -5a_2 \end{cases} $$

$$ \begin{cases} -15a_2 + 2a_2 = 0 \\ \\ a_1 = -5a_2 \end{cases} $$

$$ \begin{cases} -13a_2 = 0 \\ \\ a_1 = -5a_2 \end{cases} $$

$$ \begin{cases} a_2 = 0 \\ \\ a_1 = -5a_2 \end{cases} $$

Conocido a₂, lo sustituimos en la segunda ecuación para obtener a₁:

$$ \begin{cases} a_2 = 0 \\ \\ a_1 = -5(0) \end{cases} $$

$$ \begin{cases} a_2 = 0 \\ \\ a_1 = 0 \end{cases} $$

La única solución del sistema es la trivial: a₁ = 0 y a₂ = 0.

Por tanto, los dos vectores son linealmente independientes.

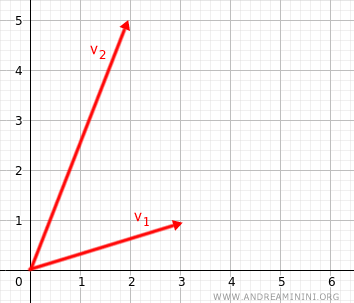
Nota. En el caso de dos vectores en el espacio bidimensional R² (es decir, en el plano), la dependencia lineal solo se da cuando los vectores son paralelos. Por tanto, si los vectores son linealmente independientes, no son vectores paralelos. Sin embargo, esta propiedad es específica del plano y no se generaliza a espacios de mayor dimensión.

Ejemplo 2

Consideremos tres vectores en el espacio vectorial real bidimensional V = R²:

$$ \vec{v_1} = \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$

$$ \vec{v_2} = \begin{pmatrix} 1 \\ 4 \end{pmatrix} $$

$$ \vec{v_3} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} $$

Estos tres vectores serán linealmente independientes si no existe ninguna combinación lineal no trivial que sea igual al vector nulo:

$$ a_1 \cdot \vec{v_1} + a_2 \cdot \vec{v_2} + a_3 \cdot \vec{v_3} = \vec{0} $$

$$ a_1 \cdot \begin{pmatrix} 3 \\ 1 \end{pmatrix} + a_2 \cdot \begin{pmatrix} 1 \\ 4 \end{pmatrix} + a_3 \cdot \begin{pmatrix} 2 \\ 1 \end{pmatrix} = \vec{0} $$

$$ \begin{pmatrix} 3a_1 \\ a_1 \end{pmatrix} + \begin{pmatrix} a_2 \\ 4a_2 \end{pmatrix} + \begin{pmatrix} 2a_3 \\ a_3 \end{pmatrix} = \vec{0} $$

Para determinar si son linealmente independientes o dependientes, planteamos el sistema de ecuaciones correspondiente:

$$ \begin{cases} 3a_1 + a_2 + 2a_3 = 0 \\ a_1 + 4a_2 + a_3 = 0 \end{cases} $$

A continuación, analizamos si el sistema admite soluciones no triviales, es decir, distintas del vector nulo de coeficientes.

Sin embargo, en este caso el sistema presenta tres incógnitas y únicamente dos ecuaciones.

Por lo tanto, según el teorema de Rouché-Capelli, el sistema posee infinitas soluciones, además de la solución trivial.

En consecuencia, los tres vectores son linealmente dependientes.

Esto implica que uno de los tres vectores puede escribirse como combinación lineal de los otros dos.

Ejemplo 3

En el espacio vectorial V = R³, definido sobre el cuerpo K = R, consideremos los siguientes dos vectores:

$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} $$ $$ v_2 = \begin{pmatrix} 3 \\ 2 \\ 3 \end{pmatrix} $$

Queremos determinar si estos vectores son linealmente dependientes.

Por definición, dos vectores son linealmente dependientes si existe una combinación lineal de ellos que sea igual al vector nulo, con al menos uno de los coeficientes α distinto de cero:

$$ \alpha_1 \cdot v_1 + \alpha_2 \cdot v_2 = \vec{0} $$

$$ \alpha_1 \cdot \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} + \alpha_2 \cdot \begin{pmatrix} 3 \\ 2 \\ 3 \end{pmatrix} = \vec{0} $$

$$ \begin{pmatrix} \alpha_1 \\ 2\alpha_1 \\ -\alpha_1 \end{pmatrix} + \begin{pmatrix} 3\alpha_2 \\ 2\alpha_2 \\ 3\alpha_2 \end{pmatrix} = \vec{0} $$

Formulamos el sistema lineal asociado, que consta de tres ecuaciones con dos incógnitas:

$$ \begin{cases} \alpha_1 + 3\alpha_2 = 0 \\ 2\alpha_1 + 2\alpha_2 = 0 \\ -\alpha_1 + 3\alpha_2 = 0 \end{cases} $$

Resolvemos el sistema para comprobar si existe una solución no trivial (es decir, con α₁ ≠ 0 y α₂ ≠ 0):

$$ \begin{cases} \alpha_1 + 3\alpha_2 = 0 \\ 2\alpha_1 + 2\alpha_2 = 0 \\ \alpha_1 = -3\alpha_2 \end{cases} $$

$$ \begin{cases} (-3\alpha_2) + 3\alpha_2 = 0 \\ 2(-3\alpha_2) + 2\alpha_2 = 0 \\ \alpha_1 = -3\alpha_2 \end{cases} $$

$$ \begin{cases} 0 = 0 \\ -4\alpha_2 = 0 \\ \alpha_1 = -3\alpha_2 \end{cases} $$

El sistema únicamente admite la solución trivial: α₁ = 0 y α₂ = 0.

Por tanto, los vectores v₁ y v₂ son linealmente independientes.

Ejemplo 4

En el mismo espacio vectorial V = R³, definido sobre el cuerpo K = R, consideremos ahora otros dos vectores:

$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} $$ $$ v_2 = \begin{pmatrix} 3 \\ 6 \\ 3 \end{pmatrix} $$

Estos vectores serán linealmente dependientes si existe una combinación lineal que sea igual al vector nulo, en la que no todos los coeficientes α sean cero simultáneamente:

$$ \alpha_1 \cdot v_1 + \alpha_2 \cdot v_2 = \vec{0} $$

$$ \alpha_1 \cdot \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} + \alpha_2 \cdot \begin{pmatrix} 3 \\ 6 \\ 3 \end{pmatrix} = \vec{0} $$

$$ \begin{pmatrix} \alpha_1 \\ 2\alpha_1 \\ -\alpha_1 \end{pmatrix} + \begin{pmatrix} 3\alpha_2 \\ 6\alpha_2 \\ 3\alpha_2 \end{pmatrix} = \vec{0} $$

Expresamos este planteamiento como un sistema lineal con tres ecuaciones y dos incógnitas:

$$ \begin{cases} \alpha_1 + 3\alpha_2 = 0 \\ 2\alpha_1 + 6\alpha_2 = 0 \\ -\alpha_1 + 3\alpha_2 = 0 \end{cases} $$

Procedemos a resolver el sistema:

$$ \begin{cases} \alpha_1 + 3\alpha_2 = 0 \\ 2\alpha_1 + 6\alpha_2 = 0 \\ \alpha_1 = -3\alpha_2 \end{cases} $$

$$ \begin{cases} (-3\alpha_2) + 3\alpha_2 = 0 \\ 2(-3\alpha_2) + 6\alpha_2 = 0 \\ \alpha_1 = -3\alpha_2 \end{cases} $$

$$ \begin{cases} 0 = 0 \\ 0 = 0 \\ \alpha_1 = -3\alpha_2 \end{cases} $$

El sistema admite soluciones no triviales.

Por tanto, los vectores v₁ y v₂ son linealmente dependientes.

Ejemplo 5

Consideremos tres vectores en el espacio vectorial V = R³:

$$ v_1 = \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} $$

$$ v_3 = \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} $$

Su combinación lineal igual al vector nulo es:

$$ a_1 \cdot \vec{v_1} + a_2 \cdot \vec{v_2} + a_3 \cdot \vec{v_3} = \vec{0} $$

$$ a_1 \cdot \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} + a_2 \cdot \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} + a_3 \cdot \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$

$$ \begin{pmatrix} 3a_1 \\ a_1 \\ -2a_1 \end{pmatrix} + \begin{pmatrix} 2a_2 \\ -a_2 \\ 0 \end{pmatrix} + \begin{pmatrix} a_3 \\ -3a_3 \\ 2a_3 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$

Convertimos la ecuación vectorial en un sistema de ecuaciones cartesianas:

$$ \begin{cases} 3a_1 + 2a_2 + a_3 = 0 \\ a_1 - a_2 - 3a_3 = 0 \\ -2a_1 + 2a_3 = 0 \end{cases} $$

Buscamos las soluciones aplicando el método de sustitución.

Despejamos a₁ en la tercera ecuación y lo sustituimos en las otras ecuaciones:

$$ \begin{cases} 3a_1 + 2a_2 + a_3 = 0 \\ a_1 - a_2 - 3a_3 = 0 \\ a_1 = a_3 \end{cases} $$

$$ \begin{cases} 3a_3 + 2a_2 + a_3 = 0 \\ a_3 - a_2 - 3a_3 = 0 \\ a_1 = a_3 \end{cases} $$

$$ \begin{cases} 4a_3 + 2a_2 = 0 \\ -a_2 - 2a_3 = 0 \\ a_1 = a_3 \end{cases} $$

Despejamos ahora a₂ en la segunda ecuación y sustituimos:

$$ \begin{cases} 4a_3 + 2a_2 = 0 \\ a_2 = -2a_3 \\ a_1 = a_3 \end{cases} $$

$$ \begin{cases} 4a_3 + 2(-2a_3) = 0 \\ a_2 = -2a_3 \\ a_1 = a_3 \end{cases} $$

$$ \begin{cases} 4a_3 - 4a_3 = 0 \\ a_2 = -2a_3 \\ a_1 = a_3 \end{cases} $$

$$ \begin{cases} 0 = 0 \\ a_2 = -2a_3 \\ a_1 = a_3 \end{cases} $$

El sistema admite infinitas soluciones, ya que a₃ puede tomar cualquier valor, determinando así los valores de a₁ y a₂.

En consecuencia, los vectores v₁, v₂ y v₃ son linealmente dependientes.

Esto significa que uno de los tres vectores puede expresarse como combinación lineal de los otros dos.

Nota. Observando los tres vectores, es evidente que el vector v₁ puede obtenerse como combinación lineal de v₂ y v₃: $$ \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} = 2 \cdot \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} - v_3 $$ $$ v_1 = 2v_2 - \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} $$

Geométricamente, esto significa que los tres vectores linealmente dependientes v₁, v₂ y v₃ pertenecen a un mismo plano en el espacio tridimensional.

 

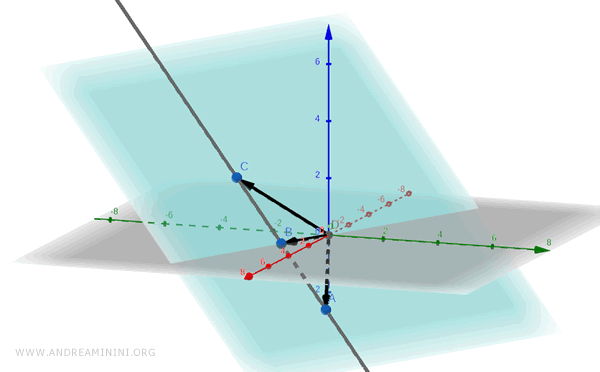
La demostración

Los vectores v₁,...,v_m son linealmente dependientes si existe una combinación lineal que sea igual al vector nulo, en la que no todos los coeficientes escalares α₁,...,α_m son simultáneamente cero:

$$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_m \cdot \vec{v}_m = \vec{0} $$

Supongamos que el coeficiente α₁ es distinto de cero:

$$ \alpha_1 \ne 0 $$

Despejamos el vector v₁, trasladando los demás términos al segundo miembro:

$$ \alpha_1 \cdot \vec{v}_1 = - \alpha_2 \cdot \vec{v}_2 \ ...\ - \alpha_m \cdot \vec{v}_m $$

Dado que α₁ ≠ 0, podemos dividir ambos miembros de la ecuación por α₁:

$$ \left( \frac{1}{\alpha_1} \right) \cdot \alpha_1 \cdot \vec{v}_1 = \left( \frac{1}{\alpha_1} \right) \cdot \left( - \alpha_2 \cdot \vec{v}_2 \ ...\ - \alpha_m \cdot \vec{v}_m \right) $$

$$ \vec{v}_1 = - \frac{ \alpha_2 }{ \alpha_1 } \cdot \vec{v}_2 \ ...\ - \frac{ \alpha_m }{ \alpha_1 } \cdot \vec{v}_m $$

Para simplificar la notación, introducimos los coeficientes β, definidos como:

$$ \beta_2 = - \frac{ \alpha_2 }{ \alpha_1 } \\ \beta_3 = - \frac{ \alpha_3 }{ \alpha_1 } \\ \vdots \\ \beta_m = - \frac{ \alpha_m }{ \alpha_1 } $$

Así obtenemos la expresión que queríamos demostrar:

$$ \vec{v}_1 = \beta_2 \cdot \vec{v}_2 + ... + \beta_m \cdot \vec{v}_m $$

Nota: Los coeficientes β son las razones: $$ \beta_2 = - \frac{ \alpha_2 }{ \alpha_1 } $$ $$ \vdots $$ $$ \beta_m = - \frac{ \alpha_m }{ \alpha_1 } $$

Veamos ahora la implicación recíproca: si el vector v₁ puede expresarse como combinación lineal de los demás,

$$ \vec{v}_1 = \beta_2 \cdot \vec{v}_2 + ... + \beta_m \cdot \vec{v}_m $$

entonces los vectores v₁, v₂,...,v_m son linealmente dependientes.

$$ - \vec{v}_1 + \beta_2 \cdot \vec{v}_2 + ... + \beta_m \cdot \vec{v}_m = \vec{0} $$

Si por hipótesis los coeficientes escalares α₂ = 0, ..., α_m = 0, entonces los correspondientes coeficientes β₂,..., β_m también serían nulos:

$$ - \vec{v}_1 + 0 \cdot \vec{v}_2 + ... + 0 \cdot \vec{v}_m = \vec{0} $$

Por tanto, la combinación lineal se reduce a:

$$ - \vec{v}_1 = \vec{0} $$

Esta no constituye una combinación lineal trivial, ya que el coeficiente de v₁ es distinto de cero (β = -1), según nuestra hipótesis inicial.

Por consiguiente, la combinación lineal es no trivial.

Corolario 1

Si los vectores v₁,...,v_m son linealmente dependientes, entonces cualquier subconjunto de ellos también es linealmente dependiente.

Demostración

Partimos de la hipótesis inicial α₁ = 1.

Por tanto, la siguiente combinación lineal es no trivial, lo que implica que los vectores son linealmente dependientes:

$$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_m \cdot \vec{v}_m = \vec{0} $$

Si suponemos que α_m = 0, podemos eliminar el último término de la combinación lineal:

$$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_{m-1} \cdot \vec{v}_{m-1} + 0 \cdot \vec{v}_m = \vec{0} $$

$$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_{m-1} \cdot \vec{v}_{m-1} = \vec{0} $$

Dado que α₁ ≠ 0 (por hipótesis), esta última combinación lineal sigue siendo no trivial.

Por consiguiente, el subconjunto correspondiente también es linealmente dependiente.

Corolario 2

Si los vectores v₁,...,v_m son linealmente dependientes, entonces cualquier conjunto de vectores { v₁,...,v_m+k } que los contenga también es linealmente dependiente, tomando α_m+1 = 0, ..., α_m+k = 0.

Demostración

$$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_m \cdot \vec{v}_m + ( \alpha_{m+1} \cdot \vec{v}_{m+1} + ... + \alpha_{m+k} \cdot \vec{v}_{m+k} ) = \vec{0} $$

$$ \text{con} \quad \alpha_{m+1} = 0 \ , \ ...\ , \ \alpha_{m+k} = 0 $$

$$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_m \cdot \vec{v}_m + ( 0 \cdot \vec{v}_{m+1} + ... + 0 \cdot \vec{v}_{m+k} ) = \vec{0} $$

$$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_m \cdot \vec{v}_m = \vec{0} $$

Dado que la combinación lineal inicial ya era no trivial, la nueva combinación lineal lo sigue siendo. Por tanto, el conjunto ampliado también es linealmente dependiente.

Cómo determinar la dependencia lineal mediante el rango de la matriz

Para determinar si un conjunto de vectores numéricos es linealmente dependiente o independiente, un método eficaz consiste en analizar el rango de la matriz asociada al sistema.

Un conjunto de n vectores numéricos v₁, ..., v_n es linealmente independiente si el rango por filas de la matriz M_m,n(R) es igual a n.
$$ r_k = n $$

El rango por columnas de una matriz M(R) corresponde al número máximo de columnas linealmente independientes, considerando dichas columnas como vectores numéricos de n componentes.

• Si r_k = n, las columnas son linealmente independientes.
• Si r_k < n, las columnas son linealmente dependientes.

Cuando las columnas son linealmente dependientes (r_k < n), es posible identificar un subconjunto de vectores independientes a partir de los menores complementarios no nulos de la matriz.

Los vectores que participan en un menor complementario con determinante distinto de cero son linealmente independientes.

Nota. Este principio también se aplica si se consideran las filas en lugar de las columnas, ya que en una matriz M_m,n(R) el rango por filas coincide con el rango por columnas.

Un ejemplo práctico

En el espacio vectorial V = R⁴, definido sobre el cuerpo K = R, consideremos los siguientes cuatro vectores:

$$ v_1 = ( 1, 0, 1, 2 ) $$ $$ v_2 = ( 1, 3, 0, 0 ) $$ $$ v_3 = ( 1, -3, 2, 4 ) $$ $$ v_4 = ( 2, 3, 1, 2 ) $$

Su combinación lineal se expresa así:

$$ \alpha_1 \cdot v_1 + \alpha_2 \cdot v_2 + \alpha_3 \cdot v_3 + \alpha_4 \cdot v_4 $$

$$ \alpha_1 \cdot ( 1, 0, 1, 2 ) + \alpha_2 \cdot ( 1, 3, 0, 0 ) + \alpha_3 \cdot ( 1, -3, 2, 4 ) + \alpha_4 \cdot ( 2, 3, 1, 2 ) $$

Disponemos estos vectores como columnas de una matriz cuadrada 4x4:

$$ M_{4,4} \begin{bmatrix} 1 & 0 & 1 & 2 \\ 1 & 3 & 0 & 0 \\ 1 & -3 & 2 & 4 \\ 2 & 3 & 1 & 2 \\ \end{bmatrix} $$

Calculamos el determinante de M_4,4:

$$ \bigtriangleup M = 0 $$

El determinante es cero, lo que implica que el rango r_k es inferior a 4.

Para determinar el rango de la matriz, aplicamos el teorema del menor complementario.

Tomamos un menor complementario de orden 2 con determinante distinto de cero:

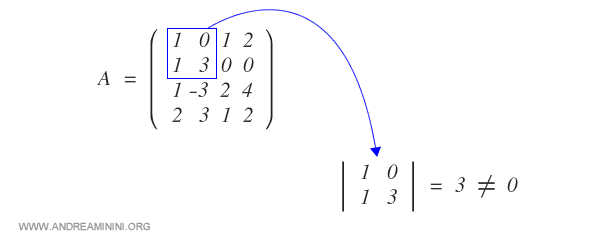
Esto indica que la matriz tiene al menos rango 2.

Para comprobar si el rango es 3, verificamos si alguno de los menores complementarios de orden 3 tiene determinante distinto de cero:

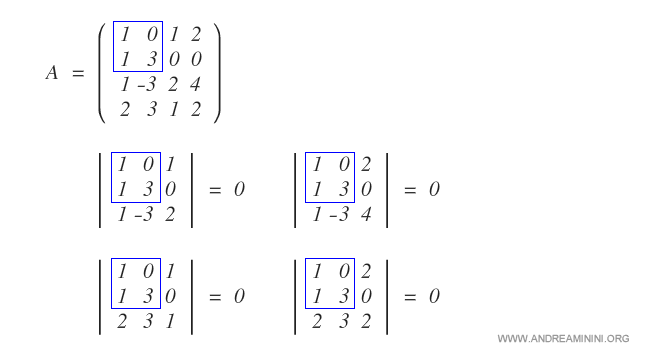
Todos los menores complementarios de orden 3 tienen determinante nulo.

Por tanto, según el teorema del menor complementario, el rango de la matriz no es 3 ni superior.

El rango de la matriz es 2.

Una vez determinado el rango, se puede establecer con claridad si los vectores son dependientes o independientes.

La matriz tiene n = 4 incógnitas (columnas), pero su rango es r_k = 2:

$$ r_k \ne n $$

Según el teorema:

1. Si r_k = n, los vectores son linealmente independientes.
2. Si r_k ≠ n, los vectores son linealmente dependientes.

Por tanto, los vectores v₁, v₂, v₃ y v₄ son linealmente dependientes.

¿Cómo identificar los vectores independientes?

Se deben seleccionar pares de vectores que formen parte de menores complementarios con determinante distinto de cero.

Por ejemplo, los vectores v₁ y v₂ son independientes, ya que pertenecen a un menor complementario cuyo determinante no es nulo:

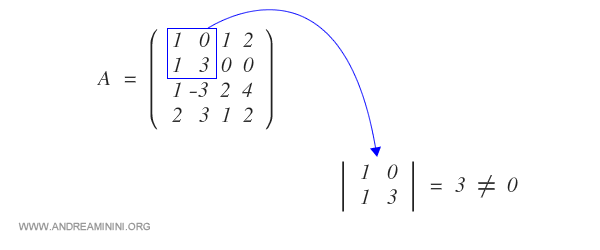
En este caso, el rango de la matriz (2) coincide con el número de columnas del menor complementario.

Este mismo procedimiento puede utilizarse para comprobar la relación de independencia entre v₂ y v₃, v₃ y v₄, v₂ y v₄, v₁ y v₃, o v₁ y v₄.

El algoritmo de eliminación de Gauss

La dependencia lineal de un conjunto de vectores también puede determinarse mediante el rango de su matriz, que se calcula aplicando el algoritmo de eliminación de Gauss-Jordan.

Según el método de Gauss, el número de pivotes en la matriz es igual a su rango.

Ejemplo

En el ejercicio anterior, los cuatro vectores se disponen como columnas en una matriz 4x4:

$$ M_{4,4} \begin{bmatrix} 1 & 1 & 1 & 2 \\ 0 & 3 & -3 & 3 \\ 1 & 0 & 2 & 1 \\ 2 & 0 & 4 & 2 \\ \end{bmatrix} $$

A continuación, transformamos la matriz en una matriz escalonada aplicando las reglas del método de Gauss:

$$ M_{4,4} \begin{bmatrix} 1 & 0 & 2 & 1 \\ 0 & 1 & -1 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} $$

Nota. Para no extender la explicación, no se detallan aquí todos los pasos intermedios de la transformación mediante el algoritmo de Gauss-Jordan. Si deseas consultar el desarrollo completo, haz clic aquí.

La matriz contiene dos pivotes, por lo que su rango es r_k = 2.

Por tanto, los vectores v₁, v₂, v₃ y v₄ son linealmente dependientes, ya que r_k < n.

Los dos vectores v₁ y v₂, correspondientes a las columnas en las que aparecen los pivotes, son linealmente independientes entre sí.

Nota. La matriz escalonada se utiliza únicamente para calcular el rango. Los valores originales de los vectores se mantienen: v₁ = ( 1, 1, 1, 2 ), v₂ = ( 0, 3, -3, 3 ), v₃ = ( 1, 0, 2, 1 ), v₄ = ( 2, 0, 4, 2 ).

Teoremas sobre la independencia lineal de los vectores

• Si un conjunto de vectores {v₁, v₂, ..., v_n} es linealmente independiente, entonces ninguno de estos vectores puede ser el vector nulo: $$ \vec{v}_1 \ne \vec{0} \\ \vec{v}_2 \ne \vec{0} \\ \vdots \\ \vec{v}_n \ne \vec{0} $$

  Véase la demostración.

• En un espacio vectorial finitamente generado V, si consideramos un conjunto generador de V $$ \{ v_1, v_2, ..., v_n \} $$ y un conjunto de vectores linealmente independientes en V $$ \{ w_1, w_2, ..., w_p \} $$, entonces se verifica que $$ p \le n $$

  Es decir, el número de vectores linealmente independientes en V no puede exceder al número de vectores de un conjunto generador de V.
  
  Véase la demostración.

Observaciones

Algunas consideraciones útiles sobre la dependencia e independencia lineal de vectores:

• El vector nulo es linealmente dependiente
  Según la definición, un vector es linealmente independiente si se anula únicamente cuando todos los coeficientes de la combinación lineal son cero (es decir, en la solución trivial α = 0): $$ \alpha \cdot \vec{v} = \vec{0} $$ Sin embargo, el vector nulo se anula para cualquier valor del coeficiente escalar α, incluso cuando α ≠ 0: $$ \alpha \cdot \vec{0} = \vec{0} $$ Por tanto, el vector nulo es siempre linealmente dependiente.

Y así sucesivamente.