Método de eliminación de Gauss
El método de eliminación de Gauss permite determinar el conjunto de soluciones posibles de un sistema de ecuaciones lineales.
Nota: Por convención, el método de Gauss se aplica a las filas de la matriz. Sin embargo, también puede aplicarse a las columnas. Por tanto, en ciertas aplicaciones prácticas es posible realizar los cálculos trabajando con columnas en lugar de filas.
Este procedimiento también es conocido como método de eliminación de Gauss-Jordan, aunque este último constituye una variante del método de Gauss.
¿Cuál es su propósito?
El método de eliminación de Gauss transforma un sistema de ecuaciones lineales en un sistema escalonado.
Esto simplifica enormemente el cálculo del rango y la resolución del sistema, especialmente en sistemas con un elevado número de ecuaciones y variables.
Funcionamiento del método de eliminación de Gauss
El objetivo de este método es obtener una matriz equivalente que resulte más sencilla de analizar.
¿Qué es una matriz equivalente? Es una matriz cuyos sistemas lineales asociados son equivalentes. Por tanto, el sistema lineal asociado a la matriz equivalente M' tiene las mismas soluciones que el sistema asociado a la matriz original M, pero su análisis resulta mucho más simple.
El proceso de eliminación de Gauss-Jordan consiste en transformar la matriz inicial en una matriz escalonada (o matriz en forma escalonada).

Cada escalón no nulo de la matriz recibe el nombre de pivote.
Nota: El pivote es el primer elemento no nulo de izquierda a derecha en una fila no nula. También se denomina término líder.
Características de una matriz escalonada
Una matriz escalonada presenta las siguientes características:
- Las filas nulas se sitúan en la parte inferior.
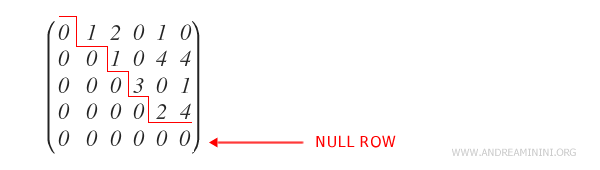
¿Qué es una fila nula? Es una fila cuyos elementos son todos iguales a cero.
- El pivote de cada fila no nula se encuentra en una columna a la derecha del pivote de la fila anterior.

Para construir la escalera de la matriz equivalente, se pueden aplicar determinadas transformaciones permitidas, conocidas como operaciones de Gauss.
¿Qué son las operaciones de Gauss?
Las operaciones permitidas sobre la matriz, según Gauss, son:
- Intercambiar dos filas.
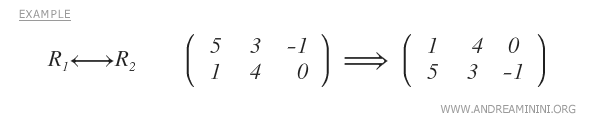
- Multiplicar una fila por un número real distinto de cero.
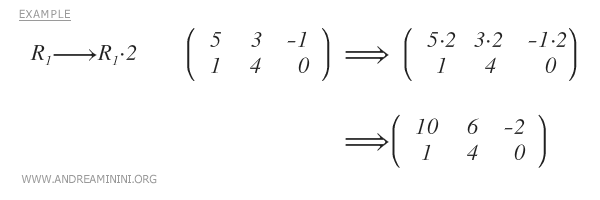
- Sumar a una fila un múltiplo de otra fila.
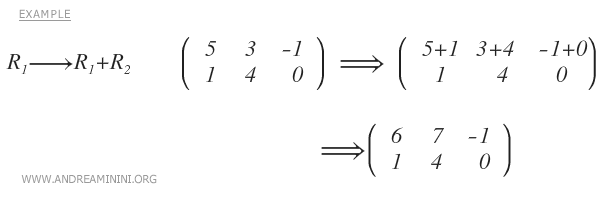
Nota: Las dos últimas operaciones pueden combinarse en una sola: sumar a una fila un múltiplo de otra fila.
Algoritmo de Gauss
Dada una matriz A de m filas y n columnas, el objetivo es obtener una matriz equivalente en forma escalonada.
Nota: Si la matriz es nula, el algoritmo concluye de inmediato.
Paso 1
Identificar la primera columna j no nula de A, de izquierda a derecha.
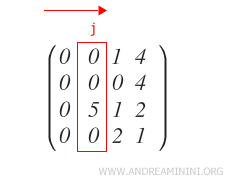
Si el primer elemento de la columna j es distinto de cero, se continúa con el paso 2.
En caso contrario, se busca la primera fila Rx que contenga un elemento j-ésimo distinto de cero.
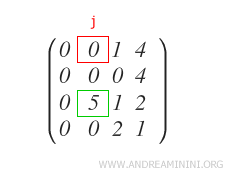
A continuación, se intercambian la fila R1 y la fila Rx y se prosigue con el paso 2.
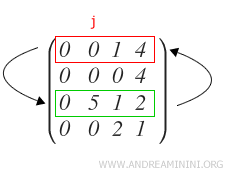
Nota: La notación para indicar esta operación de intercambio de filas es la siguiente:

De este modo se obtiene el primer pivote (p1) de la matriz.
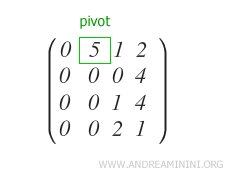
Paso 2
Se debe garantizar que los demás elementos qj-ésimos de las filas Ri situadas por debajo del pivote sean todos iguales a cero.
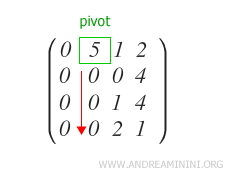
Si no es así y existen elementos no nulos, se aplica la siguiente resta a la fila Ri.
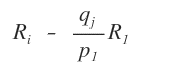
Este procedimiento permite eliminar cualquier elemento no nulo que se encuentre por debajo del pivote.
Una vez alcanzada la última fila, se continúa con el paso 3.
Paso 3
Identificar la primera columna j, situada a la derecha del último pivote, que contenga algún elemento no nulo en las filas por debajo de dicho pivote.
Si no existe tal columna, el algoritmo concluye.
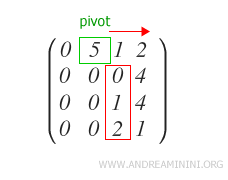
En este caso, la columna sí existe.
El primer elemento de la columna es cero. Por tanto, se busca la primera fila inferior que contenga un valor no nulo y se intercambian las filas correspondientes.
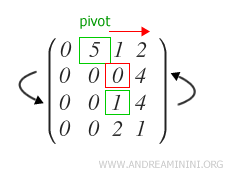
Así se determina el segundo pivote p2 de la matriz escalonada.

Si el pivote se encuentra en la última fila de la matriz (m), el algoritmo concluye en este punto.
En este caso, nos encontramos en la segunda fila (R2) de cuatro, por lo que el proceso continúa con el paso 4.
Paso 4
Verificar que los demás elementos qj-ésimos de las filas Ri situadas por debajo del último pivote pk sean todos iguales a cero.
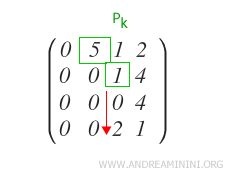
En este caso se encuentra un elemento no nulo en la fila Ri (i = 4).
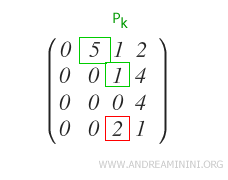
Para eliminarlo, se aplica la siguiente resta a la fila Ri.
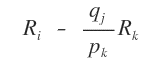
Se aplica esta fórmula a todos los elementos de la fila.
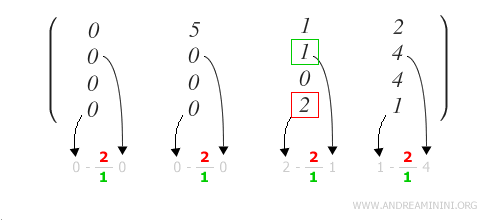
Nota: No es necesario aplicarla a los primeros elementos de la fila, ya que se anulan automáticamente debido a los ceros de la fila pivote. Sin embargo, para mayor claridad he optado por mostrar la aplicación a toda la fila.
Una vez realizados los cálculos, se obtiene la siguiente situación:

De este modo se obtiene una matriz escalonada.
Y así sucesivamente.