Matrices equivalentes
Dos matrices se consideran equivalentes cuando comparten el mismo conjunto de soluciones, S, en sus respectivos sistemas de ecuaciones lineales.
Ejemplo

La equivalencia entre dos matrices, M y M′, se denota con el símbolo de la virgulilla (~).
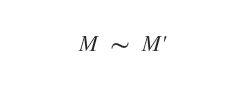
Ejemplo
Las matrices suelen emplearse para representar sistemas de ecuaciones lineales.

Reordenar las ecuaciones de un sistema lineal no modifica su conjunto de soluciones.
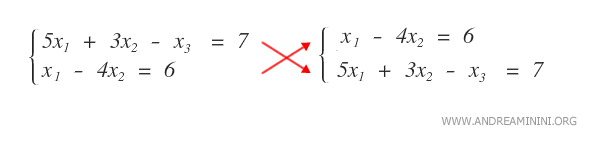
De manera análoga, cambiar el orden de las filas de una matriz da lugar a otra matriz equivalente.
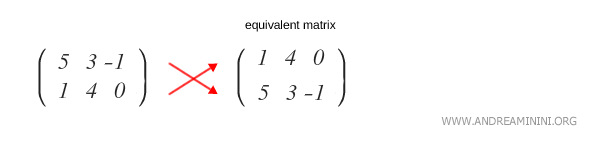
Nota: Este es un ejemplo simplificado, pensado para ilustrar el concepto con claridad. En la práctica, dos matrices equivalentes pueden diferir completamente en sus entradas. Existen diversos métodos para transformar matrices, entre los cuales destacan la eliminación de Gauss y la eliminación de Gauss-Jordan.
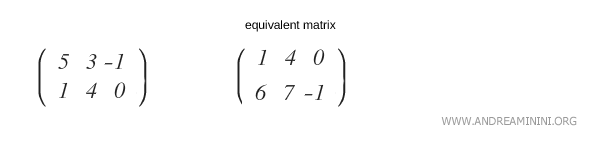
Cómo obtener una matriz equivalente
Mediante el procedimiento de eliminación de Gauss, es posible transformar cualquier matriz M en una matriz equivalente M′ aplicando una secuencia de operaciones elementales, conocidas como operaciones de Gauss.
- Intercambiar dos filas de la matriz
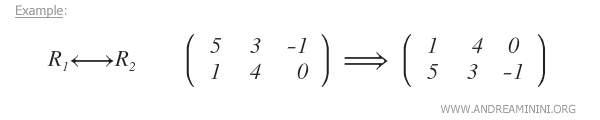
- Multiplicar una fila por un número real distinto de cero α
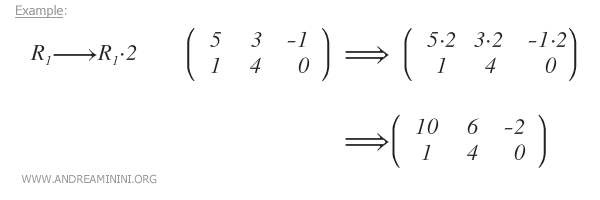
- Sumar a una fila el resultado de multiplicar otra por un número real
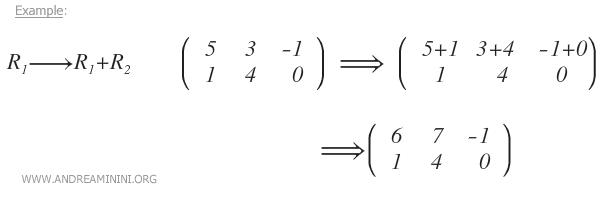
Si dos polinomios tienen una raíz común, esa raíz también estará presente en su suma. Por lo tanto, las soluciones de los polinomios originales siguen siendo válidas para la combinación resultante.
Nota: Estas operaciones pueden combinarse entre sí. Por ejemplo, se puede sumar a una fila otra fila previamente multiplicada por un número real.