Singularidad de una matriz
La singularidad de una matriz es una propiedad que se relaciona directamente con el determinante de una matriz cuadrada.
¿Qué es una matriz singular?
Una matriz cuadrada A se considera singular si su determinante, det(A), es igual a cero. En otras palabras, una matriz es singular cuando su determinante se anula.
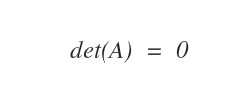
Matriz no singular
Por el contrario, una matriz cuadrada A es no singular si su determinante, det(A), es distinto de cero.
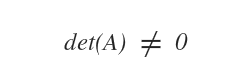
¿Por qué es importante la singularidad?
La singularidad de una matriz permite determinar si esta es invertible.
Una matriz cuadrada es invertible si, y solo si, no es singular.