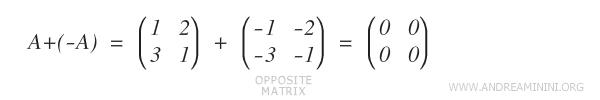Suma de matrices

¿Cómo se suman dos matrices?

Para sumar dos matrices A y B con las mismas dimensiones (m filas por n columnas), basta con sumar cada par de elementos correspondientes: a_ij + b_ij. El resultado es una nueva matriz del mismo tamaño.

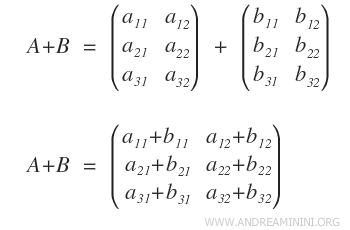
¿Se pueden sumar matrices con dimensiones distintas? No, la suma solo está definida cuando ambas matrices tienen el mismo número de filas (m) y columnas (n).

Ejemplo de suma de matrices

Veamos un ejemplo con dos matrices A y B.

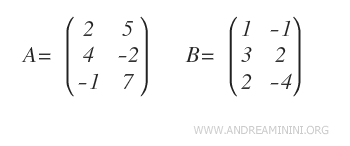
Como ambas tienen dimensiones 3×2, es posible sumarlas para obtener A + B.

La matriz A + B se obtiene sumando elemento a elemento, es decir, sumando a_ij + b_ij en cada posición correspondiente.

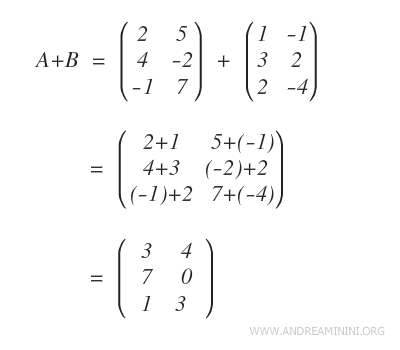
El resultado final es una nueva matriz que representa la suma de A y B.

Propiedades de la suma de matrices

La operación de suma de matrices cumple con las siguientes propiedades fundamentales:

1. Propiedad asociativa
   Para cualquier trío de matrices del mismo tamaño, se cumple que A + (B + C) = (A + B) + C.
2. Propiedad conmutativa
   El orden de los sumandos no altera el resultado: A + B = B + A.
   
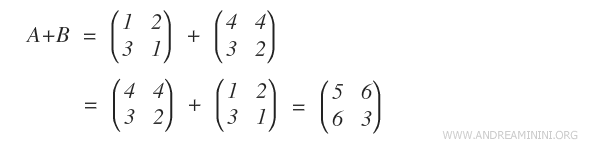
3. Existencia del elemento neutro
   Existe una matriz neutra, llamada matriz nula O, tal que A + O = A para cualquier matriz A.
   

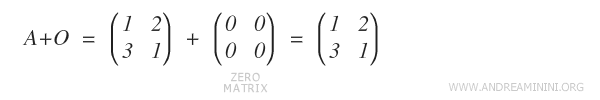
   Nota: La matriz nula es una matriz de m x n cuyos elementos son todos ceros.

4. Existencia del elemento opuesto
   Para cada matriz A existe una matriz opuesta -A tal que A + (−A) = O, donde O es la matriz nula.