Matrices semejantes

En el contexto de las matrices cuadradas de orden n, se dice que dos matrices A y B son semejantes si existe una matriz invertible M tal que:

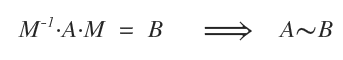
En este caso, la relación de semejanza entre las matrices se denota mediante el símbolo ~ (tilde).

La semejanza constituye una relación de equivalencia sobre el conjunto de todas las matrices de orden n.

Propiedades de las matrices semejantes

1. Toda matriz es semejante a sí misma.
2. Si una matriz A es semejante a B, entonces B también es semejante a A.
3. Si A es semejante a B y B es semejante a C, entonces A es semejante a C.
4. Las matrices semejantes comparten los mismos valores propios (autovalores), así como el mismo determinante, rango y traza.
5. Desde el punto de vista algebraico, las matrices semejantes representan el mismo endomorfismo respecto de distintas bases B₁ y B₂ de un mismo espacio vectorial V.
6. Las matrices semejantes tienen el mismo polinomio característico.

Ejemplo práctico de matrices semejantes

Consideremos las siguientes matrices A y B:

$$ A = \begin{pmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{pmatrix} $$

$$ B = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

Estas matrices son semejantes porque existe una matriz invertible M tal que:

$$ M = \begin{pmatrix} 1 & 1 & 1 \\ -2 & 1 & 0 \\ 1 & 1 & -1 \end{pmatrix} $$

y su inversa:

$$ M^{-1} = \begin{pmatrix} \frac{1}{6} & -\frac{1}{3} & \frac{1}{6} \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{2} & 0 & -\frac{1}{2} \end{pmatrix} $$

cumple que:

$$ M^{-1} A M = B $$

De hecho:

$$ \begin{pmatrix} \frac{1}{6} & -\frac{1}{3} & \frac{1}{6} \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{2} & 0 & -\frac{1}{2} \end{pmatrix} \begin{pmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{pmatrix} \begin{pmatrix} 1 & 1 & 1 \\ -2 & 1 & 0 \\ 1 & 1 & -1 \end{pmatrix} = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$