Submatrices

Una submatriz se obtiene al seleccionar determinadas filas y columnas de una matriz dada, respetando estrictamente el orden original en el que aparecen.

Ejemplo de submatriz generada a partir de una matriz original

Definición de submatriz: Sean \( I = \{1, \dots, m\} \) y \( J = \{1, \dots, n\} \) subconjuntos de \( \mathbb{Z} \), y sea \( A = (a_{ij}) \) una matriz de orden \( m \times n \), con \( i \in I \) y \( j \in J \). Si tomamos \( H \subseteq I \) y \( K \subseteq J \), la submatriz correspondiente se denota \( A_{HK} = (a_{ij}) \), donde \( i \in H \) y \( j \in K \).

Ejemplo práctico

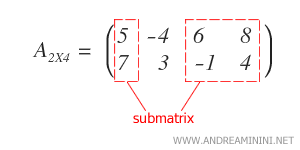
Consideremos una matriz \( A_{2 \times 4} \), es decir, una matriz con dos filas (\( m = 2 \)) y cuatro columnas (\( n = 4 \)).

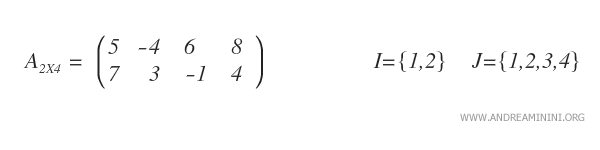
Ejemplo de una matriz rectangular de dimensiones 2x4

Seleccionando subconjuntos específicos \( H \) y \( K \) de \( I \) y \( J \), se construye una submatriz \( A_{HK} \).

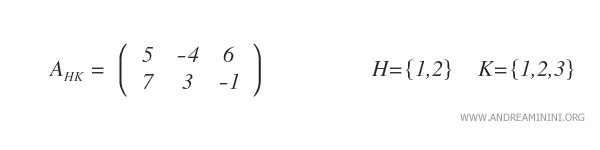
Ejemplo de submatriz extraída de A

Nota: En este caso se han seleccionado las tres primeras columnas, omitiendo la última.
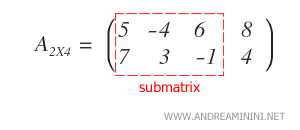
Submatriz formada con las columnas 1, 2 y 3

Es fundamental señalar que las filas y columnas elegidas no necesitan ser contiguas.

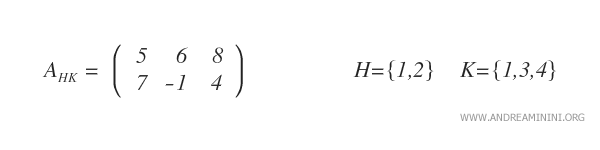
Demostración de cómo construir una submatriz a partir de columnas no consecutivas

Nota: En este ejemplo, la submatriz se ha generado seleccionando las columnas primera, tercera y cuarta.
Submatriz obtenida con columnas 1, 3 y 4

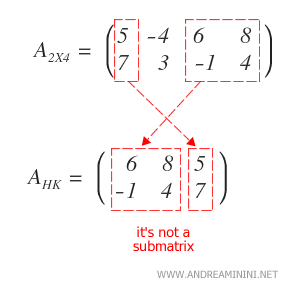
Lo esencial es que la submatriz conserve el orden relativo de filas y columnas tal como aparece en la matriz original.

Ejemplo: Si se altera el orden de las columnas seleccionadas, la matriz resultante deja de ser una submatriz en sentido estricto, aunque contenga los mismos valores. No se considera una submatriz válida porque se ha modificado el orden de las columnas.
Ejemplo de matriz que no califica como submatriz por cambio en el orden de columnas