Potencia de una matriz
La potencia de una matriz se obtiene al multiplicarla repetidamente por sí misma, combinando sus filas con las columnas en cada paso.
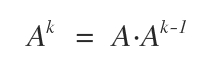
Si \( A \) es una matriz cuadrada de orden \( n \) y \( k \) es un entero no negativo, la potencia \( A^k \) se define como el producto de \( A \) por sí misma \( k-1 \) veces.
Nota: Elevar una matriz a una potencia no implica elevar cada uno de sus elementos por separado. Esto solo ocurre en casos especiales, como con las matrices diagonales.
Ejemplo de potenciación matricial
Consideremos la matriz cuadrada \( A \) de orden 2 que aparece a continuación. Vamos a calcular su tercera potencia.
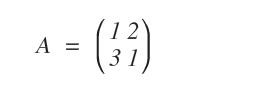
Para obtener \( A^3 \), multiplicamos la matriz \( A \) tres veces por sí misma.
El siguiente gráfico ilustra paso a paso cómo se realiza esta operación.
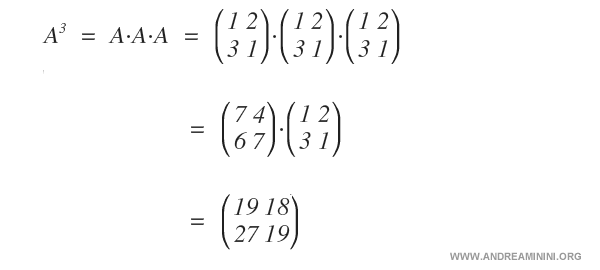
Nota: Como se observa, \( A^3 \) no consiste en elevar cada elemento al cubo, ya que la multiplicación matricial (fila por columna) sigue reglas distintas a la multiplicación escalar.
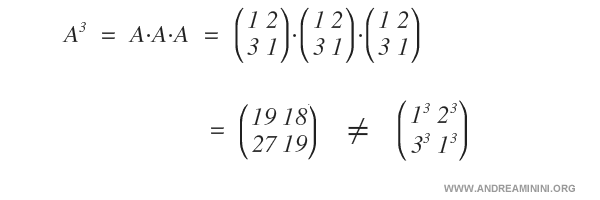
Matrices nilpotentes e idempotentes
Una matriz cuadrada \( A \) de orden \( n \) se dice nilpotente de orden \( k \) si \( A^k = O \), donde \( O \) es la matriz nula.
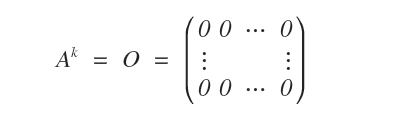
La siguiente matriz es un ejemplo de matriz nilpotente.
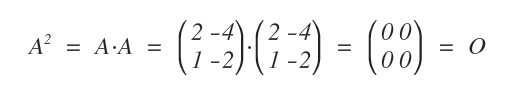
Por otro lado, una matriz cuadrada \( A \) es idempotente si existe un entero positivo \( k \) tal que \( A^k = A \).

A continuación, se muestra un ejemplo de matriz idempotente.
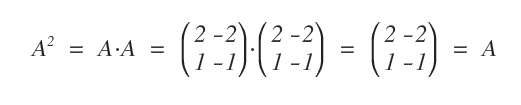
Nota: Las propiedades nilpotente e idempotente se aplican exclusivamente bajo las reglas de multiplicación matricial, es decir, multiplicación fila por columna.
Potencia cero de una matriz
Por convención, cualquier matriz cuadrada \( A \) de orden \( n \) elevada a la potencia cero se define como la matriz identidad \( I \) del mismo orden.
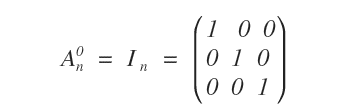
Potencias negativas de una matriz
Si el exponente \( k \) es negativo, la potencia \( A^k \) se calcula como el producto de la inversa de \( A \), \( A^{-1} \), multiplicada \( |k| \) veces.
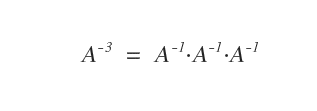
Potencias de matrices diagonales
En el caso particular de matrices diagonales, la potenciación consiste en elevar cada elemento de la diagonal a la potencia correspondiente. Este comportamiento es exclusivo de este tipo de matrices.
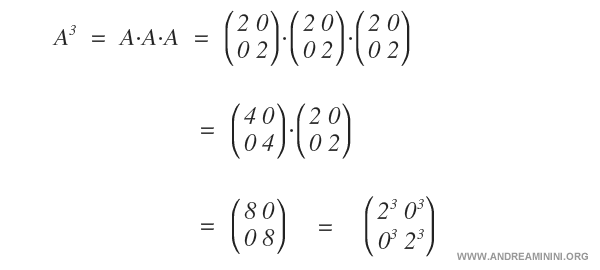
Para matrices no diagonales, la potencia de la matriz no se obtiene elevando individualmente los elementos.
Potencias binomiales de matrices
La regla del binomio que se aplica a números reales no es válida para matrices. La potenciación matricial sigue principios distintos.
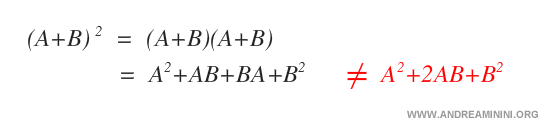
Nota: Esta es otra evidencia de que las potencias matriciales no se comportan como las potencias numéricas, y requieren un enfoque específico para su cálculo.