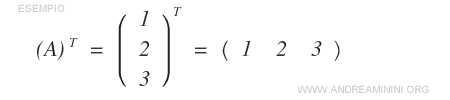Transpuesta de una matriz

¿En qué consiste la transpuesta de una matriz?

La transpuesta de una matriz se obtiene intercambiando sus filas por columnas. Si \( A = (a_{ij}) \) es una matriz real de dimensión \( m \times n \), su transpuesta, denotada por \( A^T \), será una matriz de dimensión \( n \times m \).

Ejemplo: Para obtener la transpuesta \( A^T \) de una matriz \( A \), basta con reescribir cada fila como una columna.

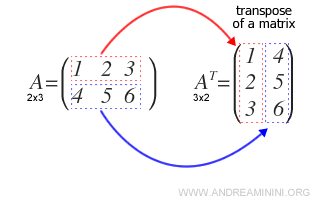
La notación \( A^T \) se emplea específicamente para indicar la transpuesta de la matriz A y no debe confundirse con una operación de potenciación.

En algunos contextos también pueden encontrarse otras notaciones, como \( t(A) \), \( A^t \) o \( ^tA \).

Propiedades de la transposición

La operación de transposición posee varias propiedades fundamentales:

1. La transpuesta de la suma de dos matrices es igual a la suma de sus transpuestas: \( (A + B)^T = A^T + B^T \).
   
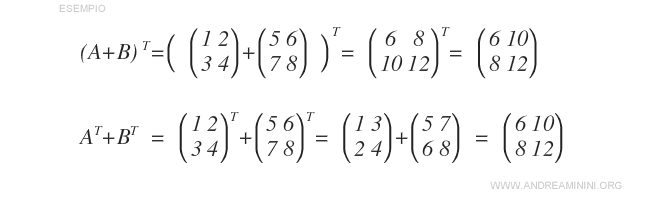
2. La transpuesta del producto de un escalar por una matriz es igual al escalar por la transpuesta de dicha matriz: \( (\alpha A)^T = \alpha A^T \).
   
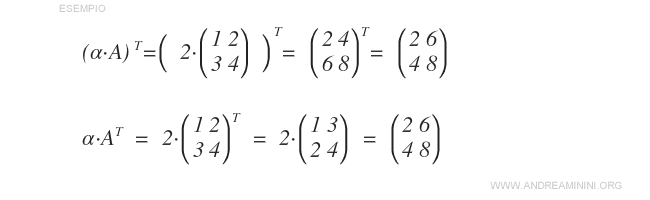
3. La transpuesta de la transpuesta de una matriz devuelve la matriz original: \( (A^T)^T = A \).
   

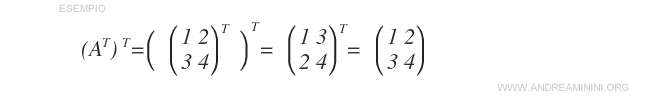
   Nota: Esta propiedad indica que la transposición es una operación involutiva.

Casos particulares

• Una matriz de dimensión \( 1 \times 1 \) es igual a su transpuesta.
  
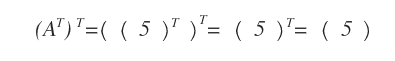
• La transpuesta de una matriz fila de dimensión \( 1 \times n \) es una matriz columna de dimensión \( n \times 1 \).
  
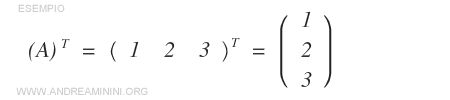
• La transpuesta de una matriz columna de dimensión \( m \times 1 \) es una matriz fila de dimensión \( 1 \times m \).