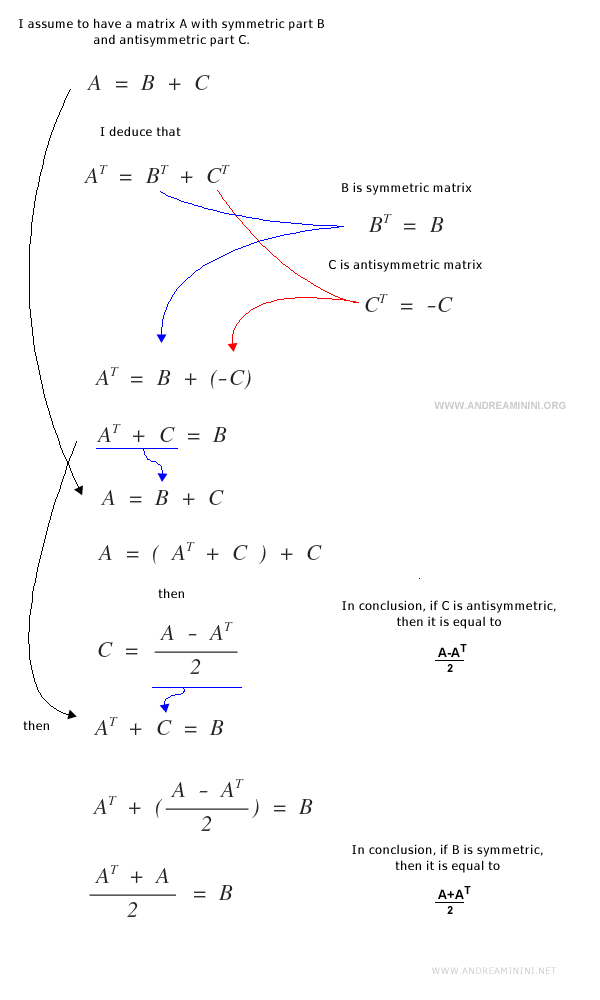
Matrices antisimétricas
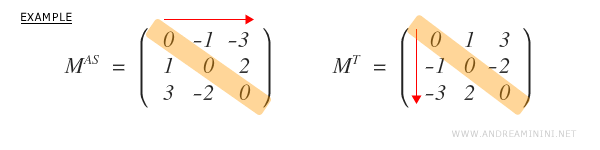
Una matriz \( M \) se denomina antisimétrica si los elementos situados por encima de la diagonal principal son iguales en valor absoluto pero de signo opuesto a los correspondientes por debajo de ella.
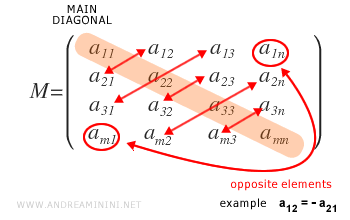
Una matriz antisimétrica suele denotarse como ASM, donde AS significa Anti Symmetric.
Ejemplo de matriz antisimétrica: Esta matriz de orden 3 ilustra claramente el concepto: cada elemento \( a_{ij} \) es igual al correspondiente \( a_{ji} \), pero con signo contrario.
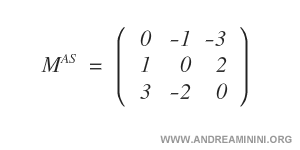
El elemento \( a_{ij} \) se obtiene intercambiando las posiciones de fila y columna: \( a_{ij} \rightarrow a_{ji} \).
En general, para toda matriz antisimétrica se cumple que \( a_{ij} = -a_{ji} \), para todo \( i, j = 1, \dots, n \).
![]()
Relación con la traspuesta
Una matriz es antisimétrica si y solo si su traspuesta es igual a su opuesto: \( M^T = -M \).
![]()
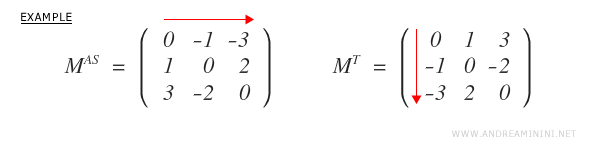
Solo las matrices cuadradas pueden ser antisimétricas
Las matrices no cuadradas no pueden ser antisimétricas, ya que su traspuesta no tiene las mismas dimensiones. Además, al no ser cuadradas, carecen de una diagonal principal bien definida.
Diagonal nula en matrices antisimétricas
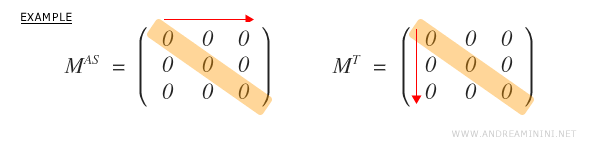
En toda matriz antisimétrica, los elementos de la diagonal principal son necesariamente nulos.
¿Por qué la diagonal debe ser cero? Porque en la traspuesta de una matriz cuadrada, los elementos de la diagonal permanecen invariantes (\( a_{ii} = a_{ii} \)). La única solución a \( a_{ii} = -a_{ii} \) es \( a_{ii} = 0 \).
¿Puede una matriz ser simultáneamente simétrica y antisimétrica?
Sí, pero solo en un caso: la matriz nula. Es la única matriz que cumple simultáneamente las condiciones de simetría y antisimetría.
Cómo obtener la parte antisimétrica de una matriz
Cualquier matriz cuadrada puede descomponerse en su parte simétrica y su parte antisimétrica.
Para obtener la componente antisimétrica de una matriz \( M \), se emplea la siguiente fórmula:
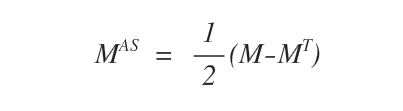
Ejemplo práctico
Consideremos la siguiente matriz cuadrada de orden 3, que no es antisimétrica:
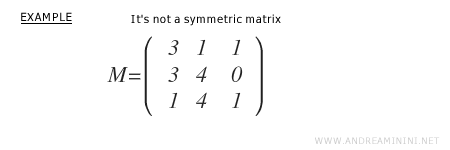
En primer lugar, calculamos su traspuesta \( M^T \).
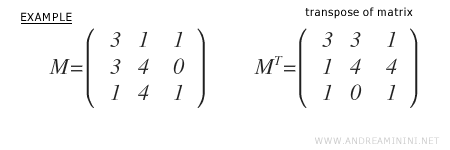
A continuación, aplicamos la fórmula \( \frac{1}{2}(M - M^T) \).
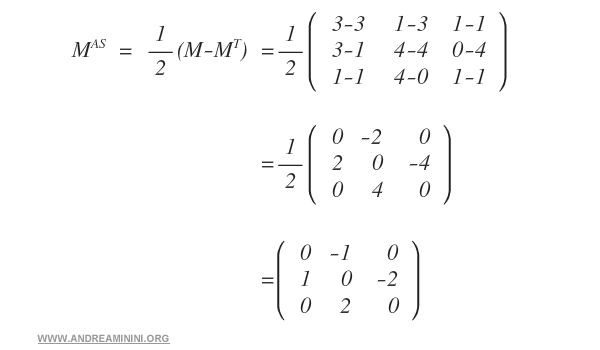
El resultado es la matriz antisimétrica asociada a \( M \), con diagonal nula y elementos opuestos simétricamente respecto a dicha diagonal.
Descomposición en partes simétrica y antisimétrica
La suma de la parte simétrica \( M^S \) y la parte antisimétrica \( M^{AS} \) de una matriz cuadrada \( M \) reconstruye la matriz original.
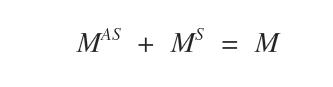
Nota: Denominamos \( M^{AS} \) a la componente antisimétrica de \( M \), y \( M^S \) a la componente simétrica. Si \( M \) es completamente simétrica, entonces \( M^{AS} = 0 \); si es completamente antisimétrica, entonces \( M^S = 0 \).
Veamos un ejemplo de cómo obtener ambas partes a partir de una matriz dada:
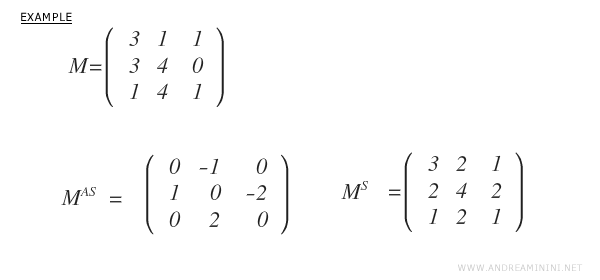
La suma de \( M^S \) y \( M^{AS} \) devuelve exactamente la matriz original \( M \).
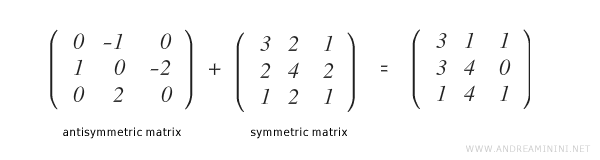
Demostración:
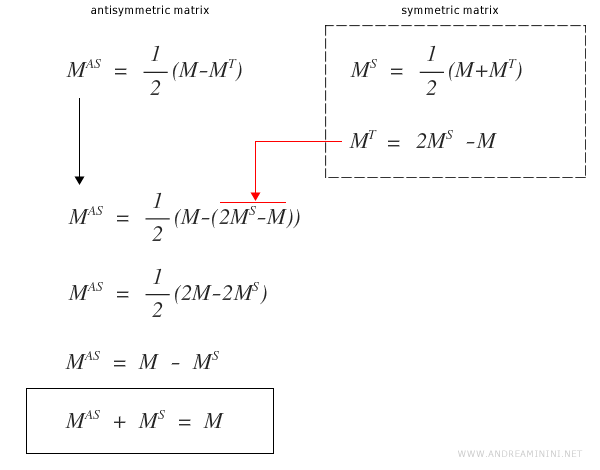
La unicidad de esta descomposición en partes simétrica y antisimétrica se justifica de manera rigurosa a continuación: