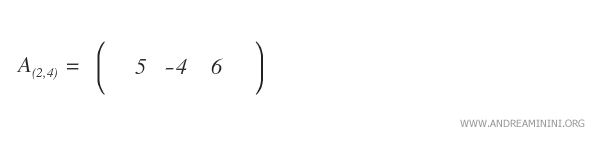Submatriz complementaria
La submatriz complementaria de un elemento \( a_{ij} \) es la matriz que se obtiene al suprimir la fila \(i\) y la columna \(j\) de la matriz original.

Dicha submatriz se denota como \( A_{(ij)} \).
Nota: La submatriz complementaria es un tipo particular de submatriz, caracterizada por la eliminación de exactamente una fila y una columna.
Ejemplo práctico
Supongamos que trabajamos con una matriz \( A_{2\times 4} \), es decir, una matriz de dos filas (\(m = 2\)) y cuatro columnas (\(n = 4\)).
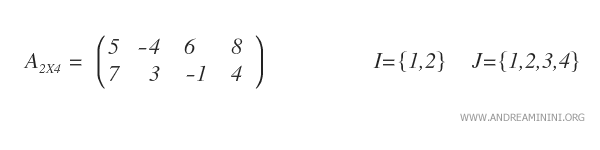
Queremos determinar la submatriz complementaria del elemento \( a_{2,4} \), ubicado en la segunda fila y cuarta columna (de valor 4).
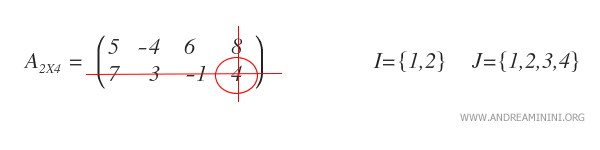
Para ello, eliminamos la segunda fila y la cuarta columna de la matriz original.
El resultado es la submatriz complementaria asociada, que denotamos como \( A_{(2,4)} \).