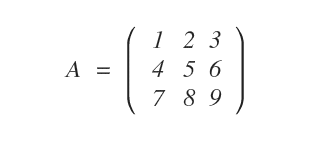Menor de una matriz
El menor de una matriz \( A \) de orden \( n \) es el determinante de una submatriz cuadrada de orden \( p \) (donde \( p \leq n \)), obtenida al eliminar \( m - p \) filas y \( n - p \) columnas de la matriz original.

Es fundamental comprender que un menor representa el determinante de una submatriz concreta (frecuentemente denominada matriz cofatora), y por tanto es un valor escalar, no una matriz en sí.
Sin embargo, en ciertos contextos también se utiliza el término “menor” para referirse a la submatriz asociada.
¿Cuál es el orden de un menor? El orden de un menor coincide con el número de filas (o columnas) de la submatriz de la cual se calcula el determinante. Por ejemplo, una submatriz de tres filas y tres columnas da lugar a un menor de tercer orden.
Cálculo de un menor
Para obtener un menor, se seleccionan \( p \) filas y \( p \) columnas de la matriz \( A \) que formarán una submatriz cuadrada.
- Identifica las filas \( i, j \) que se eliminarán de la matriz.
- La submatriz resultante se denomina matriz cofatora \( A_{ik} \).
- El determinante de dicha submatriz constituye el menor correspondiente.
Nota: Los índices \( i \) y \( j \) indican qué filas y columnas se excluyen de \( A \) para construir la submatriz cuadrada.
Los menores de primer orden se reducen a un único elemento de la matriz original.
Ejemplo práctico
Consideremos la siguiente matriz de 3×3. Calcularemos algunos de sus menores como ejemplo.
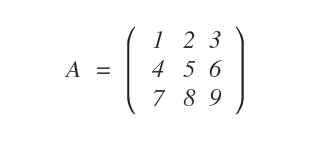
Nota: Aunque la matriz original no siempre sea cuadrada, todo menor se calcula a partir de una submatriz cuadrada (o de un único valor en el caso de orden 1).
Esta matriz tiene tres filas (\( m = 3 \)) y tres columnas (\( n = 3 \)), por lo que admite menores de hasta tercer orden.
Menores de segundo orden
Para calcular un menor de segundo orden (\( p = 2 \)), es necesario eliminar una fila (\( m - p = 1 \)) y una columna (\( n - p = 1 \)).
A continuación, se determina el determinante de la submatriz resultante.

Explicación: Al calcular el menor \( A_{31} \), se elimina la tercera fila (7, 8, 9) y la primera columna (1, 4, 7). Los elementos restantes - situados en las filas 1 y 2, y las columnas 2 y 3 - forman la submatriz cuadrada correspondiente. Aplicando este mismo procedimiento, se pueden calcular los demás menores de segundo orden.
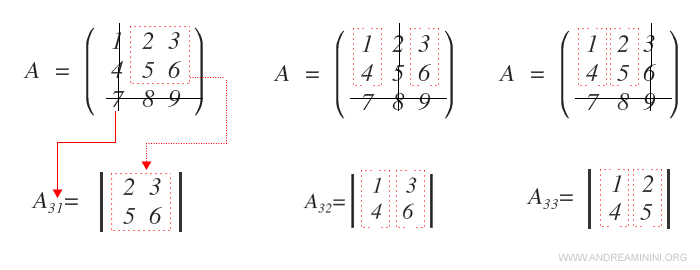
Menores de primer orden
La matriz también posee nueve menores de primer orden.
Para obtener un menor de orden 1 (\( p = 1 \)), se eliminan dos filas y dos columnas en cada caso.
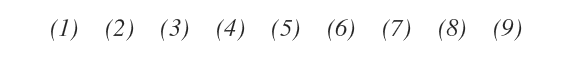
En estos casos, el menor es simplemente el valor del único elemento que queda en la submatriz.
Nota: El menor de tercer orden corresponde al determinante de la matriz completa. Para calcularlo (\( p = 3 \)), no se elimina ninguna fila ni columna.