Matrices invertibles e inversas

En álgebra lineal, una matriz cuadrada $ A $ de orden $ n $ se denomina invertible si existe otra matriz cuadrada del mismo orden, llamada matriz inversa y denotada por $ A^{-1} $, tal que $ A \cdot A^{-1} = I $ y $ A^{-1} \cdot A = I $, donde $ I $ es la matriz identidad.

matriz invertible

En notación matricial, la inversa se indica mediante el exponente −1, de forma análoga a la notación del inverso multiplicativo en aritmética.

Nota. El concepto de matriz inversa es análogo al del recíproco de un número real: todo número real distinto de cero tiene un inverso multiplicativo $ \frac{1}{a} $ tal que $ a \cdot \frac{1}{a} = 1 $. Del mismo modo, si una matriz $ M $ es invertible, existe $ M^{-1} $ tal que $ M \cdot M^{-1} = I $, donde $ I $ actúa como el neutro multiplicativo: $ M \cdot I = M $.

No todas las matrices son invertibles. De hecho, muchas matrices carecen de inversa.

El conjunto de todas las matrices invertibles de orden $ n $ con coeficientes reales se denota $ \text{GL}_n(\mathbb{R}) $ o $ \text{GL}(n, \mathbb{R}) $.

$$ \text{GL}(n, \mathbb{R}) $$

Este conjunto se conoce como el grupo lineal general de orden $ n $ sobre los reales.

Nota. El conjunto $ \text{GL}_n(\mathbb{R}) $ es cerrado respecto al producto: el producto de dos matrices invertibles del mismo orden también es una matriz invertible. Además, la matriz identidad $ I $ pertenece a $ \text{GL}_n(\mathbb{R}) $.

Ejemplo práctico de matriz inversa
Cálculo de la matriz inversa: dos métodos
Propiedades de las matrices inversas

Ejemplo práctico de matriz inversa

Consideremos la siguiente matriz:

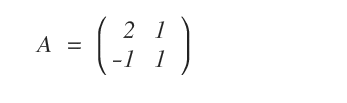
una matriz

Esta matriz es invertible, es decir, existe una matriz $ A^{-1} $ tal que $ A \cdot A^{-1} = I_{(2)} $, siendo $ I_{(2)} $ la matriz identidad de orden 2.

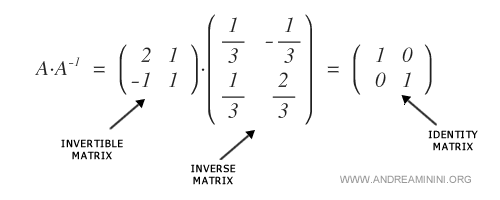
ejemplo

Cálculo de la matriz inversa: dos métodos

Existen dos enfoques principales para calcular la inversa de una matriz invertible:

Nota. El segundo método suele ser más eficiente desde el punto de vista computacional, mientras que el primero proporciona una mejor comprensión conceptual de la relación entre matrices y sistemas lineales.

Método 1

Dada una matriz $ A $, queremos determinar si es invertible y, en caso afirmativo, calcular su inversa $ A^{-1} $.

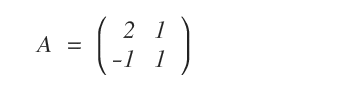
Ejemplo de matriz:

Si $ A $ es invertible, debe cumplirse que $ A \cdot A^{-1} = I $.

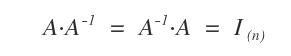
Matriz invertible:

Para verificar si $ A $ es invertible, se multiplica por una matriz $ B $ con entradas desconocidas y se impone que el producto sea igual a la identidad.

Producto de A con una matriz de incógnitas igual a la identidad

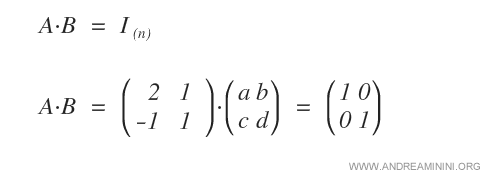
Al desarrollar el producto fila por columna se obtiene un sistema de ecuaciones lineales.

Sistema de ecuaciones lineales equivalente

Resolver este sistema permite determinar las entradas de $ A^{-1} $. Si el sistema es compatible determinado, la matriz $ A $ es invertible.

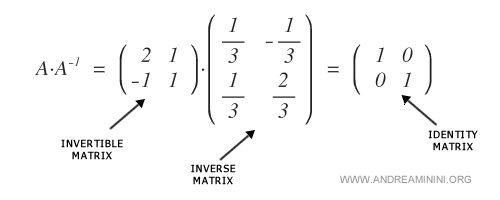
Cálculo de la matriz inversa:

Nota. Aunque este método es ilustrativo y didáctico, se vuelve poco práctico para matrices de orden superior. En estos casos, se recomienda el segundo método.

Método 2

Para una matriz $ 1 \times 1 $, su inversa es simplemente $ A^{-1} = a_{11}^{-1} $. Para matrices de mayor orden, se utiliza la fórmula: $$ A^{-1} = \frac{1}{\det(A)} \cdot \text{adj}(A) $$ donde $ \text{adj}(A) $ es la matriz adjunta.

El teorema de existencia establece que una matriz es invertible si, y solo si, su determinante es distinto de cero.

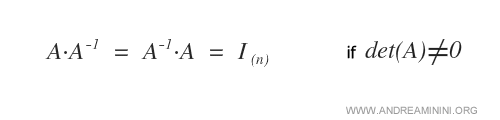
Teorema de existencia de matriz inversa:

Cuando $ \det(A) \neq 0 $, la matriz es invertible. Para calcular su inversa, se sigue el procedimiento: 1) se construye la matriz de cofactores, 2) se transpone para obtener la adjunta, 3) se multiplica por el escalar $ \frac{1}{\det(A)} $.

Nota. Si $ \det(A) = 0 $, la matriz no es invertible y no se puede continuar con el procedimiento.

Propiedades de las matrices inversas

Solo las matrices cuadradas pueden ser invertibles. Si una matriz es invertible, su inversa es única.
La inversa de una matriz no se obtiene invirtiendo cada elemento individualmente. Sus entradas pueden ser muy distintas de las de $ A $, aunque en casos particulares puedan coincidir. Por ejemplo, la inversa de la matriz identidad es ella misma.
Si $ A $ es invertible, entonces $ A^{-1} $ también lo es, y se cumple: $ (A^{-1})^{-1} = A $.
El determinante de $ A^{-1} $ es el inverso del determinante de $ A $: $$ \det(A^{-1}) = \frac{1}{\det(A)} $$
La transpuesta de una matriz invertible también es invertible: $$ (A^{T})^{-1} = (A^{-1})^{T} $$
Si $ A $ y $ B $ son matrices invertibles, entonces su producto también lo es, y: $$ (AB)^{-1} = B^{-1}A^{-1} $$
Una matriz con determinante nulo no es invertible. Solo las matrices no singulares (con determinante distinto de cero) admiten inversa.
La existencia de la inversa implica su unicidad.