Cálculo de la matriz inversa mediante eliminación de Gauss
La eliminación de Gauss es un procedimiento alternativo para obtener la inversa de una matriz.
Resulta especialmente práctica cuando la matriz es de gran tamaño y las fórmulas directas se vuelven poco manejables.
Procedimiento paso a paso: invertir una matriz con eliminación de Gauss
El primer paso consiste en colocar la matriz identidad I a la derecha de la matriz M.
Así se construye la matriz ampliada, que se denota como M|I.
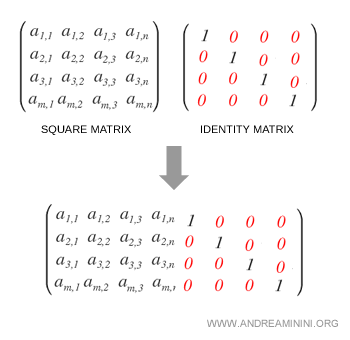
En esta matriz ampliada, la identidad aparece en el bloque derecho (marcada en rojo).
El objetivo es aplicar operaciones elementales por filas hasta transformar el bloque izquierdo en la matriz identidad.

Nota. Las operaciones elementales de fila son: intercambiar dos filas, multiplicar una fila por un escalar no nulo k, y sumar a una fila un múltiplo de otra.
Si el bloque izquierdo se convierte en la identidad, el bloque derecho será entonces la matriz inversa de M.

Un ejemplo resuelto
Consideremos la matriz 2×2:
$$ M = \begin{pmatrix} 2 & 1 \\ -1 & 1 \end{pmatrix} $$
Queremos calcular su inversa, M-1, utilizando la eliminación de Gauss.
Añadimos la identidad 2×2 a la derecha:
$$ M|I = \begin{pmatrix} 2 & 1 & 1 & 0 \\ -1 & 1 & 0 & 1 \end{pmatrix} $$
Ahora transformaremos el bloque izquierdo en la identidad aplicando operaciones de fila.
Primero, intercambiamos las dos filas: R1 ⇔ R2
$$ M|I = \begin{pmatrix} -1 & 1 & 0 & 1 \\ 2 & 1 & 1 & 0 \end{pmatrix} $$
A continuación, sumamos el doble de la primera fila a la segunda: R2 = R2 + 2·R1
$$ M|I = \begin{pmatrix} -1 & 1 & 0 & 1 \\ 2 + (-1) \cdot 2 & 1 + 1 \cdot 2 & 1 + 0 \cdot 2 & 0 + 1 \cdot 2 \end{pmatrix} $$
$$ M|I = \begin{pmatrix} -1 & 1 & 0 & 1 \\ \color{red}0 & 3 & 1 & 2 \end{pmatrix} $$
Eliminamos ahora el elemento situado encima del 3 restando un tercio de la segunda fila a la primera: R1 = R1 + (−1/3)·R2
$$ M|I = \begin{pmatrix} -1 - 0 \cdot \frac{1}{3} & 1 - 3 \cdot \frac{1}{3} & 0 - 1 \cdot \frac{1}{3} & 1 - 2 \cdot \frac{1}{3} \\ 0 & 3 & 1 & 2 \end{pmatrix} $$
$$ M|I = \begin{pmatrix} -1 & \color{red}0 & - \frac{1}{3} & \frac{1}{3} \\ 0 & 3 & 1 & 2 \end{pmatrix} $$
Multiplicamos la primera fila por −1: R1 = (−1)·R1
$$ M|I = \begin{pmatrix} -1 \cdot (-1) & 0 \cdot (-1) & - \frac{1}{3} \cdot (-1) & \frac{1}{3} \cdot (-1) \\ 0 & 3 & 1 & 2 \end{pmatrix} $$
$$ M|I = \begin{pmatrix} \color{red}1 & 0 & \frac{1}{3} & - \frac{1}{3} \\ 0 & 3 & 1 & 2 \end{pmatrix} $$
Finalmente, dividimos la segunda fila entre 3: R2 = (1/3)·R2
$$ M|I = \begin{pmatrix} 1 & 0 & \frac{1}{3} & - \frac{1}{3} \\ 0 \cdot \frac{1}{3} & 3 \cdot \frac{1}{3} & 1 \cdot \frac{1}{3} & 2 \cdot \frac{1}{3} \end{pmatrix} $$
$$ M|I = \begin{pmatrix} 1 & 0 & \frac{1}{3} & - \frac{1}{3} \\ 0 & \color{red}1 & \frac{1}{3} & \frac{2}{3} \end{pmatrix} $$
En este punto, el bloque izquierdo ya coincide con la matriz identidad.
$$ M|I = \begin{pmatrix} \color{red} 1 & \color{red}0 & \frac{1}{3} & - \frac{1}{3} \\ \color{red}0 & \color{red}1 & \frac{1}{3} & \frac{2}{3} \end{pmatrix} $$
Por lo tanto, M es efectivamente invertible.
La matriz inversa corresponde al bloque derecho:
$$ M^{-1} = \begin{pmatrix} \frac{1}{3} & - \frac{1}{3} \\ \frac{1}{3} & \frac{2}{3} \end{pmatrix} $$
Nota. También resolví este pequeño “problema de muestra” mediante otros métodos para calcular inversas, y naturalmente el resultado fue el mismo.