Cálculo de la matriz inversa con el método de Gauss - Jordan
En esta sección aplicamos el método de eliminación de Gauss - Jordan para calcular la matriz inversa A-1 de una matriz cuadrada A que sea invertible.
¿Qué es el método de Gauss - Jordan? Es un procedimiento sistemático que permite reducir una matriz a forma escalonada por filas o a forma escalonada reducida por filas.
Cómo obtiene una inversa el método de Gauss - Jordan
El proceso comienza ampliando la matriz A con la identidad, formando la matriz por bloques [A | I].
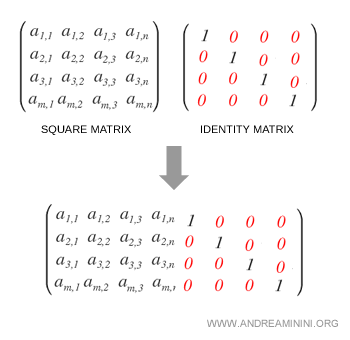
Posteriormente, el algoritmo transforma esta matriz ampliada en [I | A-1].
Nota. Las operaciones de fila permitidas son: intercambiar dos filas, multiplicar una fila por un escalar distinto de cero, y sumar a una fila un múltiplo de otra. Estas operaciones se pueden combinar según convenga. El método de Gauss - Jordan las aplica de forma secuencial para anular todos los elementos no pivote.

Si el bloque de la izquierda se convierte en la identidad, entonces el bloque de la derecha es la matriz inversa de A.

El algoritmo determina de forma precisa la secuencia de operaciones que deben realizarse, lo que lo convierte en un método idóneo para cálculos sistemáticos.
¿En qué se diferencia Gauss - Jordan de la eliminación gaussiana? En ambos casos, la idea es trasladar la identidad desde el bloque derecho al izquierdo para obtener la inversa. Con la eliminación gaussiana, el orden de las operaciones puede elegirse libremente, lo cual resulta práctico para cálculos manuales. En cambio, Gauss - Jordan prescribe una secuencia fija de pasos, por lo que es más adecuado para procedimientos automatizados.
Ejemplo resuelto
Consideremos una matriz cuadrada A y busquemos su inversa A-1:
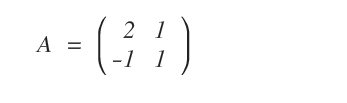
Ampliamos A con la matriz identidad I del mismo orden (2 en este caso):
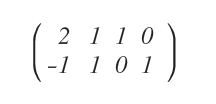
El objetivo es desplazar la identidad hacia la izquierda mediante operaciones elementales de fila.
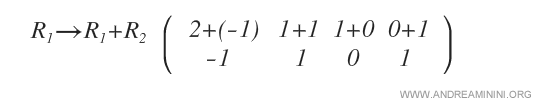
Así obtenemos el primer pivote: un 1 en la diagonal principal.

Después eliminamos el elemento situado debajo del pivote (−1) aplicando la fórmula de Gauss - Jordan.
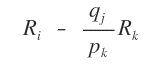
Aquí \( q_j \) es el elemento a eliminar (−1), \( p_k \) el pivote (1), y \( R_i \) y \( R_k \) la fila que se actualiza y la fila del pivote, respectivamente.
La razón es \( q_j / p_k = -1 \):
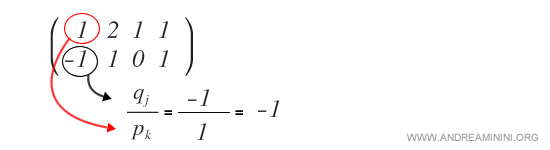
Aplicamos \( R_2 - (q_j/p_k)\cdot R_1 \) a cada elemento de la fila 2. El factor (−1) se aplica de forma uniforme a toda la fila.
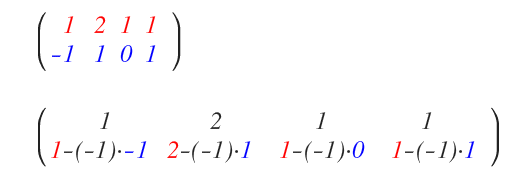
De este modo, la columna bajo el pivote queda anulada. La primera columna queda ya completada.

Pasamos ahora a la segunda columna. El pivote aquí es 3, que normalizamos a 1 multiplicando la fila 2 por 1/3:
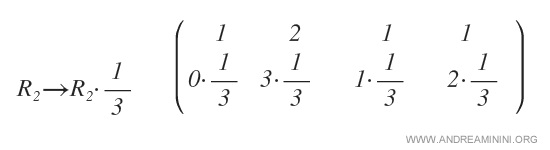
Así obtenemos el segundo pivote: el 1 en la segunda posición de la diagonal.

Aún queda un elemento distinto de cero sobre el pivote (2 en la primera fila). Para eliminarlo aplicamos \( R_1 - (q_j/p_k)\cdot R_2 \). Aquí \( q_j = 2 \) y \( p_k = 1 \), de modo que la razón es 2:
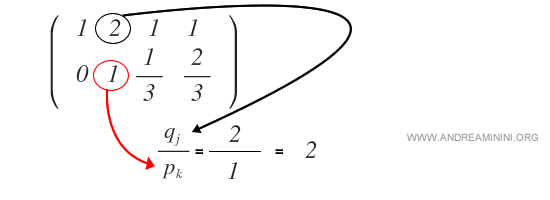
Aplicamos la operación a la fila 1:
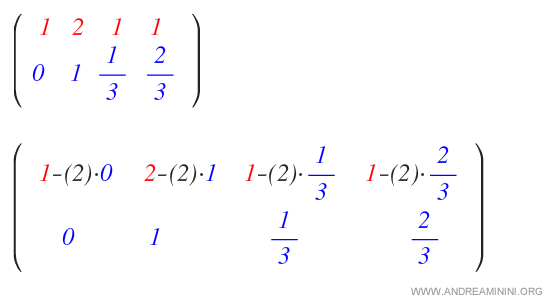
Así se elimina el 2 de la segunda columna.
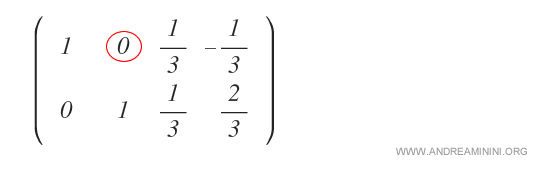
En este punto, el bloque de la izquierda ya es la matriz identidad.
Por lo tanto, la matriz A es invertible, y el bloque derecho corresponde a su inversa A-1:
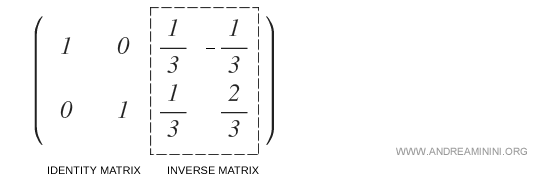
La matriz inversa de A es, entonces:
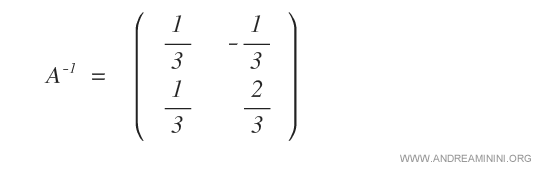
Para verificarlo, multiplicamos A por A-1. El producto es la identidad I:
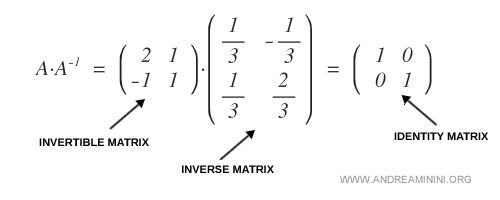
Nota. También resolví este ejemplo aplicando otros métodos para calcular la inversa, y en todos los casos obtuve el mismo resultado.