Grupo Lineal General
El Grupo Lineal General
En álgebra lineal, el grupo lineal general (GL) es el conjunto de todas las matrices invertibles de orden n sobre un cuerpo K. También se le conoce como grupo matricial y se denota por GL(n,K) o GLn(K).
La noción de grupo lineal general fue introducida por primera vez en 1832 por Évariste Galois.
Una matriz es invertible si es no singular, es decir, cuando su determinante es distinto de cero.
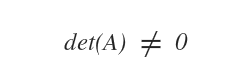
De este modo, el grupo lineal general (GL) de matrices reales invertibles de orden n se define de la siguiente manera:
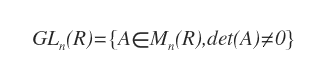
Explicación. Toda matriz A de orden n con determinante distinto de cero pertenece al grupo lineal general GL.
Ejemplo
La siguiente matriz es un ejemplo de elemento del grupo lineal general de orden 2.
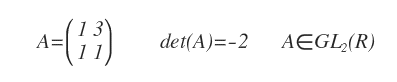
Grupo Lineal Especial
El grupo lineal especial (SL) está formado por matrices cuadradas reales de orden n cuyo determinante es igual a uno. Se trata de un subgrupo de GL.
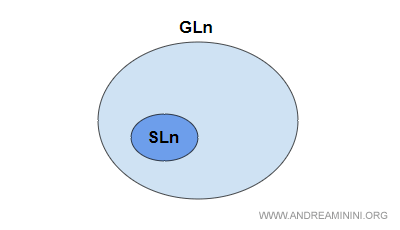
Este grupo se denota como SL(n,K) o bien SLn(K).
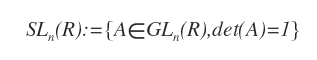
Explicación. Toda matriz A perteneciente a GLn con determinante igual a uno forma parte también del grupo lineal especial SLn.
Ejemplo
La siguiente matriz pertenece al grupo lineal especial de orden 2.
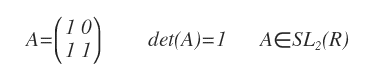
El Grupo Ortogonal Especial
El grupo ortogonal especial es un subgrupo del grupo lineal especial SLn, formado por las matrices ortogonales reales de orden n con determinante igual a 1.
Se denota por SOn.
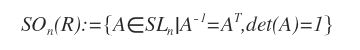
En otras palabras, el grupo ortogonal especial puede describirse como la intersección entre el grupo lineal especial SLn y el conjunto On de matrices ortogonales de orden n.
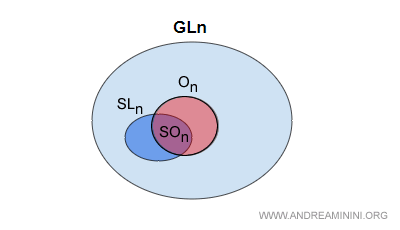
Diferencia entre el grupo ortogonal especial y el grupo ortogonal general. El grupo ortogonal especial SOn es un subgrupo de SLn. En cambio, el grupo ortogonal general On está formado por todas las matrices ortogonales con determinante +1 o −1. A su vez, On constituye un subgrupo del grupo lineal general GLn.
Ejemplo
La siguiente matriz es un elemento del grupo ortogonal especial SO2 de orden 2.
