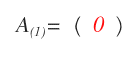Matriz cuadrada

Una matriz cuadrada es aquella que tiene el mismo número de filas y columnas (m = n). Este tipo de matriz, también llamado de orden n, suele representarse con el símbolo A(n).

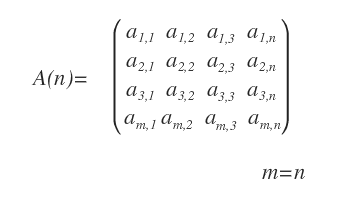
Aplicaciones de las matrices cuadradas Las matrices cuadradas poseen propiedades particulares que las convierten en herramientas clave dentro del Álgebra Lineal.

Diagonales de una matriz cuadrada

Las matrices cuadradas presentan dos diagonales bien definidas:

1. Diagonal principal: En una matriz cuadrada de orden n, la diagonal principal está formada por los elementos a_i,i con i = 1, ..., n. Recorre la matriz desde la esquina superior izquierda hasta la inferior derecha.
   
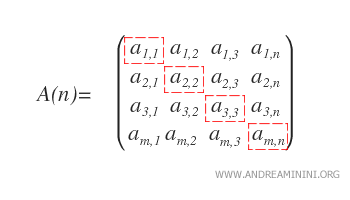
2. Diagonal secundaria: Esta diagonal incluye los elementos a_i,i para i = n, ..., 1, y va desde la esquina superior derecha hasta la inferior izquierda.
   

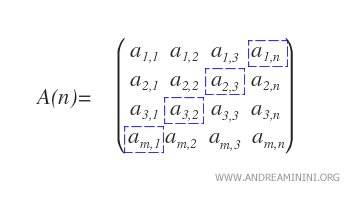
Nota: Solo las matrices cuadradas tienen diagonales. Las matrices rectangulares, fila, columna o nulas carecen de ellas.

Matrices diagonales, triangulares superiores e inferiores

Las matrices cuadradas pueden clasificarse, según la posición de sus elementos no nulos, en diagonales, triangulares superiores o triangulares inferiores:

• Matrices triangulares superiores: Una matriz es triangular superior si a_ij = 0 para todo i > j, es decir, todos los elementos situados por debajo de la diagonal principal son cero.
  
  

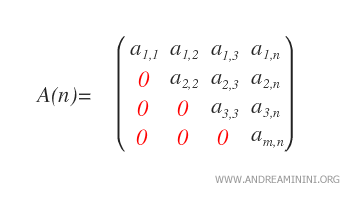
  El conjunto de matrices triangulares superiores reales de orden n se denota como U_n(R).

  Matrices estrictamente triangulares superiores: Una matriz es estrictamente triangular superior si a_ij = 0 para todo i ≥ j, es decir, todos los elementos en y por debajo de la diagonal principal son nulos.
  
  Este conjunto se representa con U*_n(R).

• Matrices triangulares inferiores: Una matriz es triangular inferior si a_ij = 0 para todo i < j, lo que implica que todos los elementos situados por encima de la diagonal principal son cero.
  
  

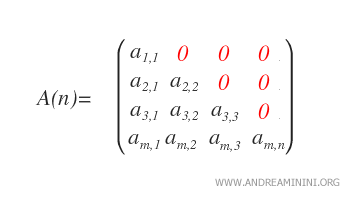
  El conjunto de matrices triangulares inferiores reales de orden n se denota como L_n(R).

  Matrices estrictamente triangulares inferiores: Una matriz es estrictamente triangular inferior si a_ij = 0 para todo i ≤ j, es decir, todos los elementos sobre y sobre la diagonal principal son cero.
  
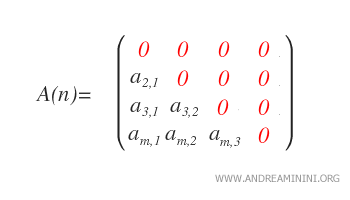
  Este conjunto se representa con L*_n(R).

• Diagonal: Una matriz cuadrada se dice diagonal si a_ij = 0 para todo i ≠ j, es decir, todos los elementos fuera de la diagonal principal son cero. Por lo tanto, una matriz diagonal es simultáneamente triangular superior e inferior.
  
  

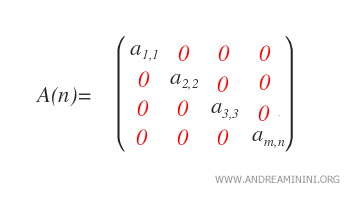
  El conjunto de matrices diagonales reales de tamaño n x n se denota como D_n(R).

Nota: Para que una matriz se considere triangular superior o inferior no se exige que los elementos fuera de la zona de ceros sean distintos de cero.

Casos especiales de matrices cuadradas en Álgebra Lineal

Un caso destacable es la matriz nula, que cumple simultáneamente con las condiciones de ser triangular superior, inferior, estrictamente superior, estrictamente inferior y diagonal.

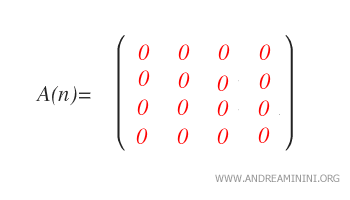
Otro caso singular es la matriz cuadrada de orden 1, compuesta únicamente por el elemento a_1,1.

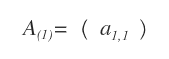
Por definición, una matriz de orden 1 siempre es triangular superior, inferior y diagonal.

Nota: Si a_1,1 = 0, entonces la matriz de orden 1 también se considera estrictamente triangular superior e inferior.