Cofactor
El cofactor (también denominado complemento algebraico) de un elemento \(a_{ij}\) es el menor de la submatriz \(A_{(ij)}\), multiplicado por el factor de signo \((-1)^{i+j}\).
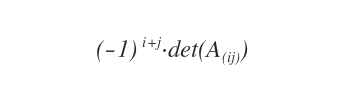
¿Cómo se calcula un cofactor?
Para calcular el cofactor de un elemento \(a_{ij}\) de una matriz \(A\), se comienza hallando su menor correspondiente.
¿Qué es el menor de un elemento? El menor asociado a un elemento \(a_{ij}\) es el determinante de la submatriz complementaria, obtenida al eliminar la fila \(i\) y la columna \(j\) de la matriz original.

Una vez calculado el menor, se multiplica por el signo correspondiente, es decir, por \((-1)^{i+j}\).
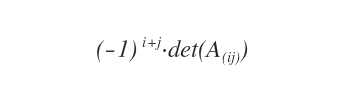
De este modo se obtiene el cofactor de \(a_{ij}\).
El signo del cofactor depende exclusivamente de la posición que ocupa el elemento dentro de la matriz.
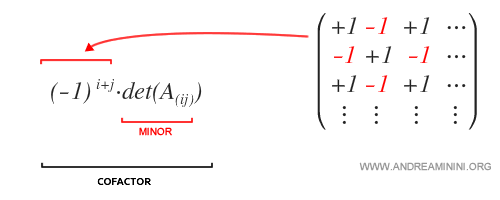
Así, en algunas posiciones el cofactor conserva el mismo signo que el menor, mientras que en otras adquiere el signo opuesto.
Ejemplo práctico
Consideremos una matriz cuadrada \(A\) de orden 3:
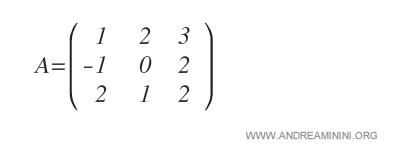
Queremos calcular el cofactor del elemento \(a_{11}\).
En primer lugar, identificamos la submatriz complementaria asociada a \(a_{11}\):
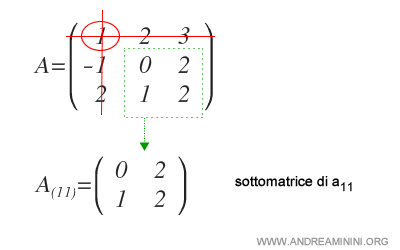
A continuación, calculamos el determinante de dicha submatriz, que constituye el menor de \(a_{11}\).
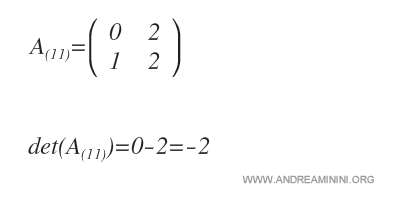
Finalmente, multiplicamos el menor por \((-1)^{i+j}\). En este caso, como \(i=1\) y \(j=1\), el signo es positivo: \((-1)^2 = +1\).
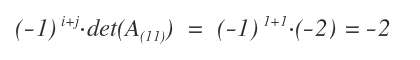
Por tanto, el cofactor de \(a_{11}\) es igual a -2.
En este ejemplo particular, el cofactor coincide en valor y signo con el menor. Sin embargo, esto no ocurre en general, ya que el signo depende de la posición del elemento.
Observación: Si calculamos el cofactor de \(a_{12}\), el signo cambiará, ya que \((-1)^{1+2} = -1\). El menor de \(a_{12}\) es -6, por lo tanto su cofactor resulta ser 6.
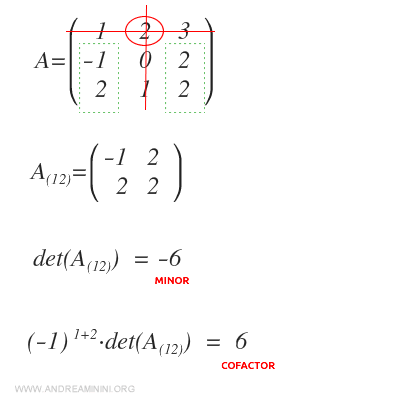
Este procedimiento puede repetirse para obtener los cofactores de todos los elementos de la matriz.