Matriz escalar

Una matriz escalar es una matriz cuadrada en la que todos los elementos de la diagonal principal tienen el mismo valor constante (distinto de cero), mientras que los elementos fuera de la diagonal son todos iguales a cero.

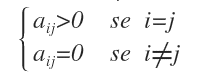
Dicho de otro modo, es un tipo particular de matriz diagonal en la que todos los valores de la diagonal principal son iguales entre sí.

Ejemplo: La siguiente matriz es un ejemplo de matriz escalar.

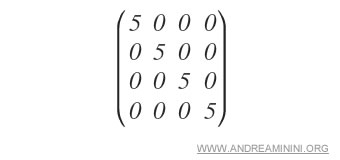
Una matriz escalar se obtiene multiplicando la matriz identidad por una constante escalar.

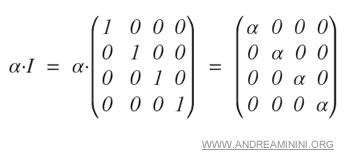
Este tipo de matriz puede expresarse siempre como un múltiplo escalar de la matriz identidad.

Dados un escalar α y la matriz identidad I, una matriz escalar es simplemente el producto α·I.

Propiedades de las matrices escalares

Las matrices escalares presentan una propiedad destacada: conmutan con cualquier matriz compatible en la multiplicación.

Para cualquier número real α, matriz escalar I(n) y matriz A de tamaño compatible, se cumple que α·I(n)·A = α·A·I(m), y en ambos casos el resultado es α·A.

Ejemplo: Aplicación práctica de una matriz escalar.