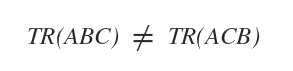Traza de una Matriz

La traza de una matriz cuadrada A de orden n es la suma de los elementos situados en su diagonal principal.

La expresión general para calcular la traza es la siguiente:

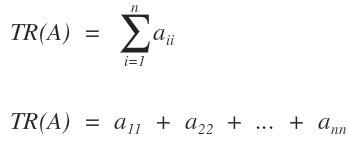
Ejemplo Práctico

Consideremos la siguiente matriz cuadrada de orden tres.

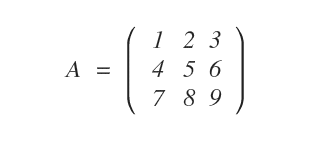
Los elementos de su diagonal principal son 1, 5 y 9.

Para obtener la traza TR(A), basta con sumar estos valores.

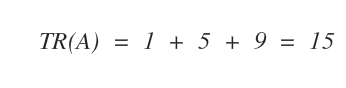
Así, la traza de la matriz A es igual a 15.

Propiedades de la Traza

La traza de una matriz cumple con las siguientes propiedades fundamentales:

1. La traza de un escalar α multiplicado por una matriz, TR(α·A), es igual al producto del escalar por la traza de la matriz: α·TR(A).
   
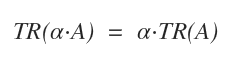
2. La suma de las trazas de dos matrices, TR(A)+TR(B), coincide con la traza de su suma: TR(A+B).
   

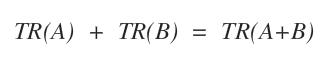
   Nota. Estas dos primeras propiedades muestran que la traza es una aplicación lineal.

3. Una matriz A y su transpuesta A^T tienen la misma traza.
   
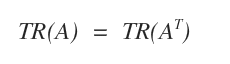
4. La traza del producto de matrices, TR(ABC), se mantiene invariante bajo permutaciones cíclicas: TR(BCA) y TR(CAB).
   

   Ejemplo de permutación no cíclica. La traza no se conserva en TR(ACB) ni en TR(CBA), ya que no son permutaciones cíclicas. En estos casos, el orden de los factores no se obtiene mediante una rotación cíclica.