Diagonal principal de una matriz cuadrada

La diagonal principal de una matriz cuadrada de orden n está compuesta por los elementos cuyas posiciones tienen el mismo índice de fila y de columna. Es decir: $$ a_{11}, \ a_{22}, \ a_{33}, \ ... , \ a_{nn} . $$

Esta diagonal se extiende desde la esquina superior izquierda hasta la esquina inferior derecha de la matriz.

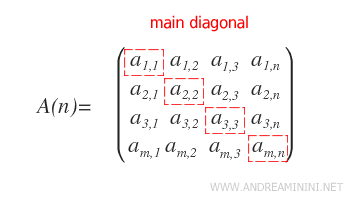
Nota: La diagonal principal solo existe en matrices cuadradas, es decir, aquellas que tienen el mismo número de filas y de columnas.

Ejemplo

Consideremos una matriz cuadrada de orden n = 3, lo que significa que tiene tres filas y tres columnas.

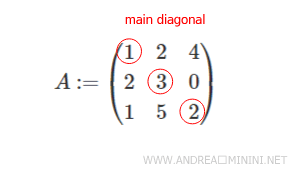
En esta ilustración se destaca la diagonal principal de una matriz 3×3.

Los elementos que pertenecen a dicha diagonal son los siguientes:

$$ a_{11} = 1 $$

$$ a_{22} = 3 $$

$$ a_{33} = 2 $$

y así sucesivamente, en función del tamaño de la matriz.