Operación de pivote en una matriz

La operación de pivote es una transformación matricial que consiste en reemplazar la columna k de una matriz de dimensiones m × n por la columna h de la matriz identidad de orden m.

Para llevar a cabo esta operación, primero se elige un elemento distinto de cero en la matriz, conocido como el elemento pivote. Si el valor es cero, no puede utilizarse como pivote.

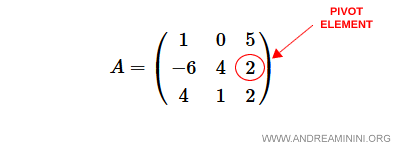
La operación de pivote se realiza en dos pasos fundamentales:

1. Se divide cada entrada de la fila h entre el elemento pivote $a_{hk}$, de modo que este último se normalice a 1: $$ \bar{a}_{h} = \frac{a_{hi}}{a_{hk}} $$
2. Se restan, a todas las demás filas $j$, la fila pivote multiplicada por el valor correspondiente en la columna pivote $a_{jk}$: $$ \bar{a}_{j} = a_{j} - a_{jk} \cdot \bar{a}_{h} $$ Este paso anula todos los elementos de la columna pivote, salvo el propio pivote.

Un ejemplo práctico

Consideremos la siguiente matriz:

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ -6 & 4 & 2 \\ 4 & 1 & 2 \end{pmatrix} $$

Tomamos como elemento pivote el valor $a_{23}$, es decir, el tercer elemento de la segunda fila.

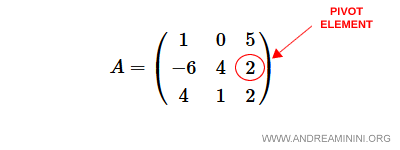
Esto implica que la tercera columna es la columna pivote y la segunda fila es la fila pivote.

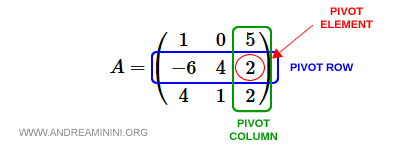
Para resaltar visualmente el pivote, lo marcamos con los símbolos <>:

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ -6 & 4 & <2> \\ 4 & 1 & 2 \end{pmatrix} $$

Dividimos ahora cada entrada de la fila pivote entre el pivote $a_{23} = 2$:

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ \frac{-6}{2} & \frac{4}{2} & <\frac{2}{2}> \\ 4 & 1 & 2 \end{pmatrix} $$

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ -3 & 2 & <1> \\ 4 & 1 & 2 \end{pmatrix} $$

La fila pivote ha sido normalizada y el elemento pivote ahora vale 1.

A continuación, restamos a cada una de las otras filas la fila pivote multiplicada por el coeficiente correspondiente de la columna pivote (k = 3).

Fila 1

La primera fila es $[1, 0, 5]$ y el valor en la columna pivote es 5.

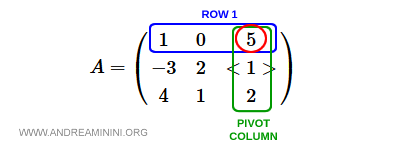
$$ a_1 = [1 \:\: 0 \:\: 5] - 5 \cdot [-3 \:\: 2 \:\: 1] $$

$$ a_1 = [1 \:\: 0 \:\: 5] - [-15 \:\: 10 \:\: 5] $$

$$ a_1 = [16 \:\: -10 \:\: 0] $$

Fila 2

Corresponde a la fila pivote y no requiere más modificaciones.

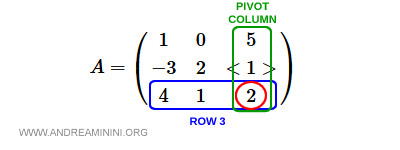
Fila 3

La tercera fila es $[4, 1, 2]$, con 2 en la columna pivote.

$$ a_3 = [4 \:\: 1 \:\: 2] - 2 \cdot [-3 \:\: 2 \:\: 1] $$

$$ a_3 = [4 \:\: 1 \:\: 2] - [-6 \:\: 4 \:\: 2] $$

$$ a_3 = [10 \:\: -3 \:\: 0] $$

Tras esta fase, las filas primera y tercera han sido actualizadas correctamente.

Resultado final

Al completar la operación de pivote sobre $a_{23}$, obtenemos la siguiente matriz:

$$ A = \begin{pmatrix} 16 & -10 & 0 \\ -3 & 2 & <1> \\ 10 & -3 & 0 \end{pmatrix} $$

El pivote se ha transformado en 1 y el resto de su columna ha sido anulado.

Otro enfoque posible

Existe una alternativa que utiliza una matriz identidad de tamaño m × m.

Si tenemos una matriz $M$ de dimensiones m × n y un pivote $a_{h,k}$, el procedimiento es el siguiente:

1. Construir una matriz identidad $Q$ de orden m.
2. Reemplazar la columna h de $Q$ con la columna k de $M$.
3. Sustituir el elemento pivote $a_{h,k}$ en $Q$ por su recíproco.
4. Multiplicar el resto de los elementos de la columna pivote por el recíproco negativo del pivote.
5. Multiplicar $Q$ por $M$ para obtener $M' = Q \cdot M$.
6. La matriz resultante $M'$ refleja la operación de pivote.

Ejemplo aplicado

Veamos cómo aplicar este método alternativo a la matriz $A$ del ejemplo anterior.

La matriz tiene $m=3$ filas y $n=3$ columnas, con pivote $a_{2,3} = 2$.

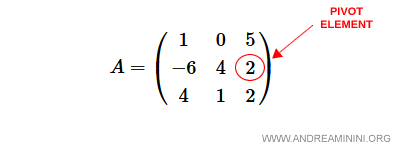
Partimos de la matriz identidad $Q$ (3 × 3):

$$ Q = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

Reemplazamos la columna h=2 de $Q$ por la columna k=3 de $A$, marcando el pivote con <>:

$$ Q = \begin{pmatrix} 1 & 5 & 0 \\ 0 & <2> & 0 \\ 0 & 2 & 1 \end{pmatrix} $$

Sustituimos el pivote por su inverso:

$$ Q = \begin{pmatrix} 1 & 5 & 0 \\ 0 & \frac{1}{<2>} & 0 \\ 0 & 2 & 1 \end{pmatrix} $$

Multiplicamos los otros valores de la columna h=2 por el opuesto del recíproco:

$$ Q = \begin{pmatrix} 1 & -\frac{5}{2} & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & -1 & 1 \end{pmatrix} $$

Finalmente, multiplicamos $Q$ por $A$:

$$ Q \cdot A = \begin{pmatrix} 1 & -\frac{5}{2} & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & -1 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 5 \\ -6 & 4 & 2 \\ 4 & 1 & 2 \end{pmatrix} $$

$$ Q \cdot A = \begin{pmatrix} 16 & -10 & 0 \\ -3 & 2 & <1> \\ 10 & -3 & 0 \end{pmatrix} $$

El resultado coincide con el obtenido mediante el método directo, confirmando la validez de este enfoque alternativo.