Matriz identidad

Una matriz identidad de orden \( n \) es una matriz cuadrada y diagonal cuyos elementos sobre la diagonal principal son todos iguales a uno, mientras que el resto de las entradas son ceros. Por esta razón, también se la denomina matriz unidad o, simplemente, matriz identidad.

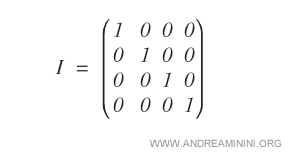
Se trata de un caso particular dentro del conjunto de las matrices diagonales, y posee propiedades únicas.

Se representa como \( I_{(n)} = (\delta_{ij}) \), donde \( n \) indica su orden y los elementos \( \delta_{ij} \) corresponden al delta de Kronecker.

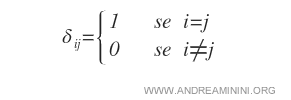
Nota: La matriz identidad es también un caso especial de matriz escalar, en el que todos los elementos de la diagonal valen exactamente uno.

Propiedades de la matriz identidad

Estas son algunas de las propiedades fundamentales de la matriz identidad:

• Actúa como elemento neutro en la multiplicación matricial. Al multiplicar cualquier matriz \( M \), que tenga \( n \) columnas, por una matriz identidad \( I \) del mismo orden, se obtiene nuevamente la matriz original: $$ M \cdot I = M $$

  Ejemplo: $$ M \cdot I_2 = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} $$

  En el caso de matrices no cuadradas, es indispensable que el número de columnas de la primera coincida con el número de filas de la segunda para que el producto esté bien definido.
  • Para cualquier matriz \( A \) con \( n \) columnas: $$ A \cdot I_n = A $$

    Ejemplo: $$ A \cdot I_2 = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} $$

  • Para cualquier matriz \( B \) con \( n \) filas: $$ I_n \cdot B = B $$

    Ejemplo: $$ I_3 \cdot A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} $$

• Con matrices cuadradas, la matriz identidad conmute en la multiplicación. Si una de las matrices \( A \) o \( B \) es la identidad, se cumple que \( AB = BA \); es decir, el orden de los factores no altera el producto.

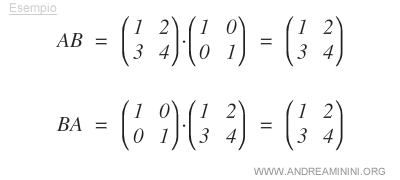
  Nota: Esta propiedad conmutativa es exclusiva de la matriz identidad. En general, la multiplicación de matrices no es conmutativa; más detalles en multiplicación de matrices.

• El determinante de una matriz identidad es siempre igual a 1: $$ \text{det}(I) = 1 $$