Matriz simétrica
¿Qué es una matriz simétrica?
Una matriz simétrica es una matriz cuadrada de orden \( n \) cuyos elementos se reflejan con respecto a la diagonal principal.
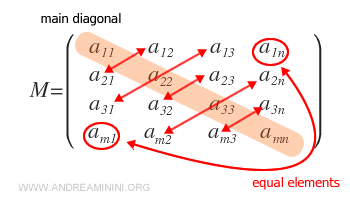
En este tipo de matrices, se cumple que \( a_{ij} = a_{ji} \) para todos los índices \( i, j = 1, ..., n \).
![]()
Nota: Solo las matrices cuadradas pueden ser simétricas. Las matrices con distinto número de filas y columnas ( \( m \neq n \) ) no pueden serlo, ya que su estructura no coincide con la de su traspuesta. Además, únicamente las matrices cuadradas tienen una diagonal principal bien definida.
Por convención, las matrices simétricas se denotan como \( M^S \), donde la "S" indica "simétrica".
El conjunto de todas las matrices simétricas se representa como \( S(n, R) \), donde \( n \) es el orden de la matriz y \( R \) es el conjunto de los números reales.
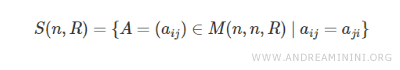
Este conjunto \( S(n, R) \) es un subconjunto del espacio de matrices cuadradas con coeficientes reales, denotado \( M(n, n, R) \).
Un ejemplo práctico
La siguiente matriz tiene tres filas ( \( m = 3 \) ) y tres columnas ( \( n = 3 \) ), por lo tanto es cuadrada ( \( m = n \) ).
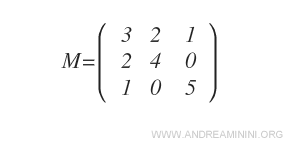
Al ser cuadrada, posee una diagonal principal bien definida.
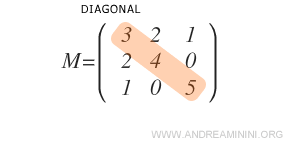
Para verificar si es simétrica, se comparan los elementos situados por encima y por debajo de la diagonal principal.
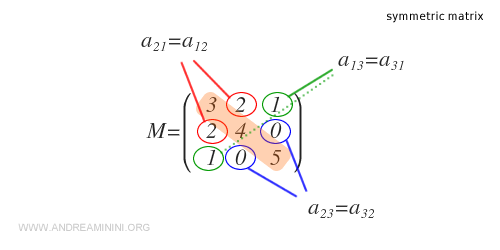
En este caso, la matriz es simétrica porque al intercambiar filas por columnas, los valores de sus elementos no cambian.
Nota: Una matriz cuadrada que no cumpla la condición de simetría no se considera simétrica.
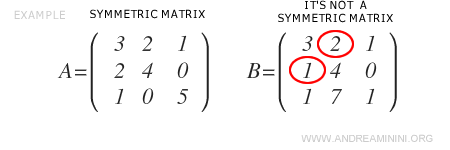
La traspuesta de una matriz simétrica
Una matriz simétrica \( M \) siempre coincide con su traspuesta \( M^T \).
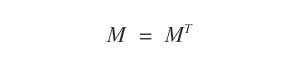
Ejemplo: La matriz \( M \) mostrada a continuación es simétrica, por lo tanto es igual a su traspuesta \( M^T \). Al intercambiar filas por columnas, cada elemento \( a_{ij} \) permanece inalterado.
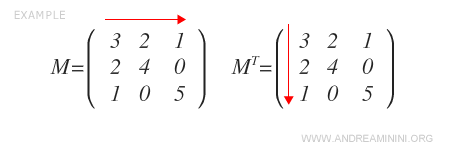
Cómo construir una matriz simétrica
Cualquier matriz cuadrada de orden \( n \) puede convertirse en una matriz simétrica.
Para obtener su forma simétrica, se utiliza la siguiente expresión:
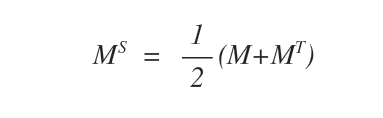
Otro ejemplo práctico
Observa esta matriz cuadrada de orden 3 que no es simétrica.
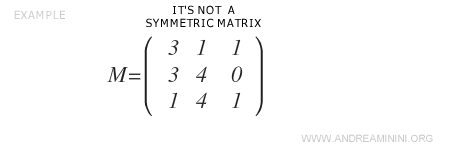
Para convertirla en una matriz simétrica, primero se calcula su traspuesta \( M^T \).
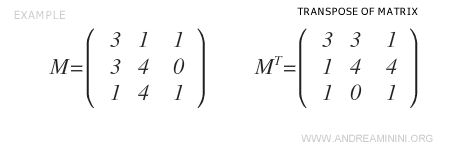
Luego se aplica la fórmula \( \frac{1}{2} \cdot (M + M^T) \).
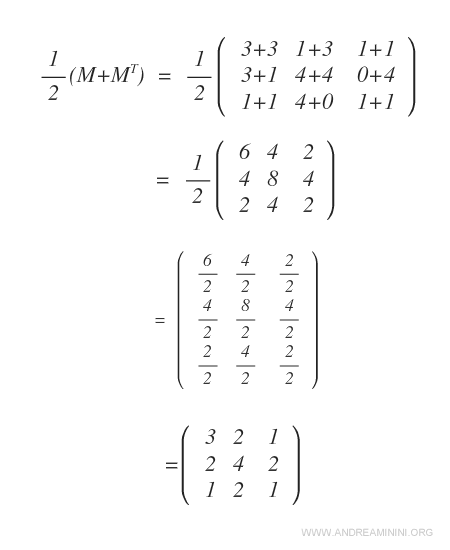
El resultado es la matriz simétrica \( M_s \), cuyos elementos están distribuidos simétricamente respecto a la diagonal principal.
Diferencias entre matrices simétricas y antisimétricas
En una matriz simétrica, se cumple que \( a_{ij} = a_{ji} \).
En cambio, en una matriz antisimétrica se cumple que \( a_{ij} = -a_{ji} \).
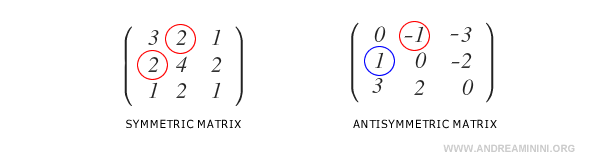
Nota: Que una matriz no sea simétrica no implica que sea antisimétrica. Los conjuntos de matrices simétricas \( S_n(R) \) y antisimétricas \( A_n(R) \) son subconjuntos distintos del espacio \( M_n(R) \). Solo comparten un elemento en común: la matriz nula, que es simultáneamente simétrica y antisimétrica.
Resumen: propiedades clave de las matrices simétricas
Entre las propiedades fundamentales de las matrices simétricas, destacan:
- Toda matriz nula es simétrica.
- La suma de una matriz simétrica \( M^S \) y una matriz antisimétrica \( M^{AS} \) permite reconstruir la matriz original \( M \).
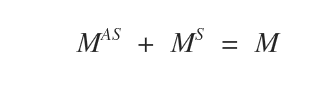
- Toda matriz diagonal \( D(n, R) \) es también una matriz simétrica \( S(n, R) \).
Demostración: Las matrices diagonales \( D(n, R) \) son cuadradas y comparten características estructurales con las simétricas \( S(n, R) \):
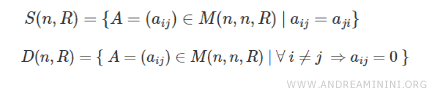
En una matriz diagonal \( D(n, R) \) se presentan dos situaciones:
1) Si \( i \neq j \), entonces \( a_{ij} = 0 \), y por lo tanto \( a_{ji} = 0 \), cumpliendo la simetría.
2) Si \( i = j \), entonces \( a_{ij} = a_{ji} \) porque se trata del mismo elemento.
En consecuencia, toda matriz diagonal es necesariamente simétrica.