Matriz adjunta
La matriz adjunta es un concepto fundamental en el álgebra matricial, con múltiples aplicaciones en diversas áreas de las matemáticas. De forma sencilla, la adjunta (también llamada matriz adjunta o adjunta traspuesta) se obtiene como la traspuesta de la matriz de cofactores de una matriz dada. En notación estándar, suele representarse como adj.
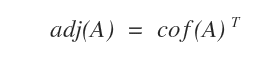
Veamos, paso a paso, cómo se calcula la matriz adjunta.
Partimos de una matriz $A$:
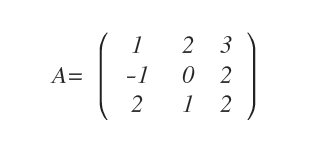
El primer paso consiste en construir la matriz de cofactores de $A$.
¿Qué son los cofactores? Los cofactores (o complementos algebraicos) se obtienen a partir de los menores de los elementos $a_{ij}$ de la matriz $A$, ajustados mediante el signo $(-1)^{i+j}$.
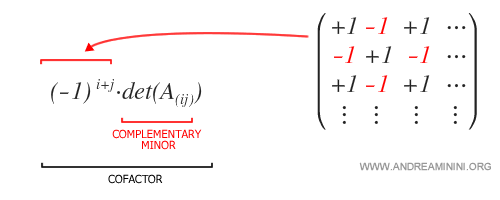
La matriz de cofactores, denotada por $\text{cof}(A)$, se construye aplicando la siguiente fórmula:
$$ \text{cof}(A) = \begin{pmatrix} (-1)^{1+1} \, \det(A_{1,1}) & (-1)^{1+2} \, \det(A_{1,2}) & (-1)^{1+3} \, \det(A_{1,3}) \\ (-1)^{2+1} \, \det(A_{2,1}) & (-1)^{2+2} \, \det(A_{2,2}) & (-1)^{2+3} \, \det(A_{2,3}) \\ (-1)^{3+1} \, \det(A_{3,1}) & (-1)^{3+2} \, \det(A_{3,2}) & (-1)^{3+3} \, \det(A_{3,3}) \end{pmatrix} $$
Reemplazamos ahora cada entrada con los determinantes de los correspondientes menores:
$$ \text{cof}(A) = \begin{pmatrix} (+1) \cdot \det \begin{pmatrix} 0 & 2 \\ 1 & 2 \end{pmatrix} & (-1) \cdot \det \begin{pmatrix} -1 & 2 \\ 2 & 2 \end{pmatrix} & (+1) \cdot \det \begin{pmatrix} -1 & 0 \\ 2 & 1 \end{pmatrix} \\ (-1) \cdot \det \begin{pmatrix} 2 & 3 \\ 1 & 2 \end{pmatrix} & (+1) \cdot \det \begin{pmatrix} 1 & 3 \\ 2 & 2 \end{pmatrix} & (-1) \cdot \det \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} \\ (+1) \cdot \det \begin{pmatrix} 2 & 3 \\ 0 & 2 \end{pmatrix} & (-1) \cdot \det \begin{pmatrix} 1 & 3 \\ -1 & 2 \end{pmatrix} & (+1) \cdot \det \begin{pmatrix} 1 & 2 \\ -1 & 0 \end{pmatrix} \end{pmatrix} $$
Evaluamos cada determinante y aplicamos el signo correspondiente:
$$ \text{cof}(A) = \begin{pmatrix} -2 & 6 & -1 \\ -1 & -4 & 3 \\ 4 & -5 & 2 \end{pmatrix} $$
La matriz adjunta se obtiene como la traspuesta de esta matriz de cofactores:
$$ \text{adj}(A) = \text{cof}(A)^T = \begin{pmatrix} -2 & -1 & 4 \\ 6 & -4 & -5 \\ -1 & 3 & 2 \end{pmatrix} $$
Esta es la matriz adjunta de $A$, resultado de transponer la matriz de cofactores.
El dominio del cálculo de la matriz adjunta resulta crucial en numerosos procedimientos matemáticos, entre ellos la obtención de matrices inversas, la resolución de sistemas de ecuaciones mediante la fórmula de Cramer y ciertas transformaciones lineales en espacios vectoriales.