Sistemas de ecuaciones lineales escalonados
Un sistema de ecuaciones lineales se denomina sistema escalonado (forma escalonada o echelon form) si puede expresar con el siguiente formato:
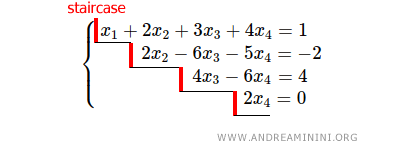
El número de incógnitas en cada ecuación disminuye progresivamente desde la primera hasta la última ecuación del sistema.
El número de escalones del sistema lineal es igual al rango de la matriz.
Este enfoque facilita el cálculo del rango, incluso en sistemas que incluyen un elevado número de ecuaciones y variables.
¿Por qué son útiles los sistemas escalonados?
Los sistemas lineales escalonados son especialmente fáciles de resolver, ya que permiten determinar los valores de las incógnitas de forma progresiva, comenzando por la última ecuación.
Si un sistema lineal no se encuentra en forma escalonada, puede transformarse aplicando el método de eliminación de Gauss-Jordan.
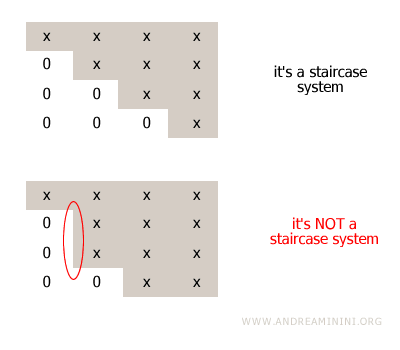
Nota. Para que un sistema sea considerado escalonado, cada pivote debe encontrarse exactamente una fila por debajo del anterior. Si se produce un salto de dos o más filas, la matriz no es escalonada.
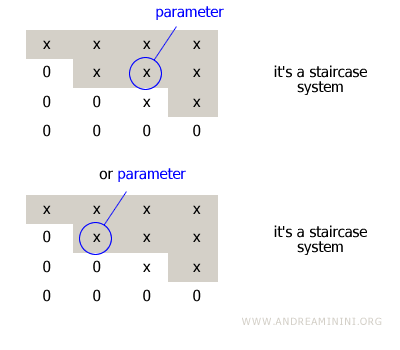
Si un escalón afecta a dos variables (columnas), una de esas variables debe tratarse como parámetro del sistema.
Ejemplo práctico
Ejemplo 1
El siguiente sistema de ecuaciones lineales es escalonado:
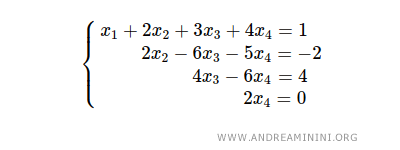
El sistema consta de 4 escalones y n = 4 incógnitas.
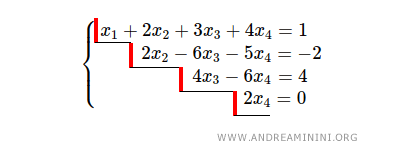
La matriz ampliada del sistema tiene rango r = 4, ya que el sistema presenta 4 escalones.
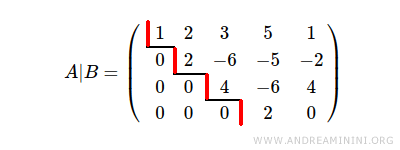
La matriz de coeficientes también tiene rango 4 por el mismo motivo.
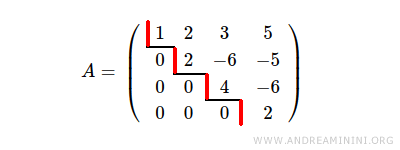
Por tanto, según el teorema de Rouché-Capelli, el sistema admite al menos una solución.
En este caso, admite una única solución, ya que el rango (r = 4) coincide con el número de incógnitas (n = 4).
$$ \infty^{n-r} = \infty^{4-4} = \infty^0 = 1 $$
El proceso de resolución comienza con la última ecuación 2x4 = 0, que se resuelve inmediatamente: x4 = 0.
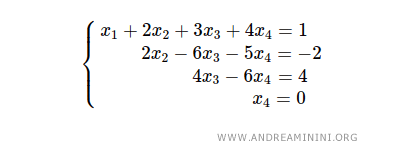
Se sustituye x4 = 0 en la tercera ecuación, obteniendo 4x3 = 4, lo que implica x3 = 1.
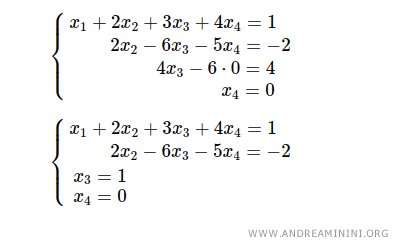
A continuación, se sustituyen x3 = 1 y x4 = 0 en la segunda ecuación: 2x2 - 6·1 - 5·0 = -2, obteniendo x2 = 2.
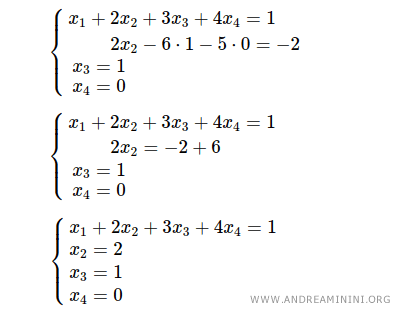
Finalmente, se sustituyen x2 = 2, x3 = 1 y x4 = 0 en la primera ecuación: x1 + 2·2 + 3·1 + 4·0 = 1, de donde se obtiene x1 = -6.
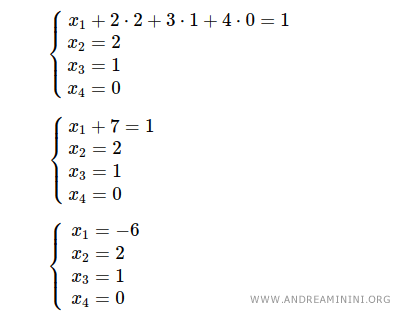
El sistema queda completamente resuelto en pocos pasos.
Las soluciones del sistema son: x1 = -6, x2 = 2, x3 = 1 y x4 = 0.
Nota. Por este motivo resulta sumamente útil transformar un sistema de ecuaciones lineales en un sistema escalonado: la resolución se vuelve mucho más sencilla, incluso cuando el sistema es grande o complejo.
Ejemplo 2
Este otro sistema de ecuaciones lineales también se encuentra en forma escalonada:
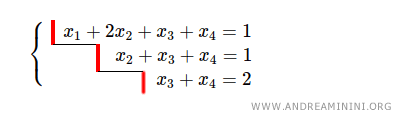
La matriz ampliada del sistema tiene rango r = 3, pues el sistema cuenta con 3 escalones.
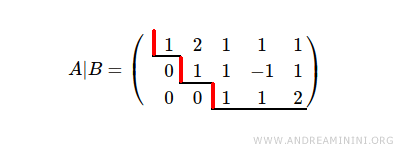
La matriz de coeficientes también presenta rango r = 3.
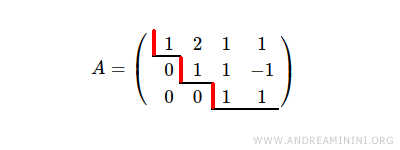
Según el teorema de Rouché-Capelli, el sistema admite una o infinitas soluciones.
En este caso, el sistema admite infinitas soluciones, ya que el rango (r = 3) es menor que el número de incógnitas (n = 4).
$$ \infty^{n-r} = \infty^{4-3} = \infty^1 = \infty $$
Para encontrar las soluciones es necesario parametrizar el sistema.
Por ejemplo, a partir de la última ecuación se puede expresar la variable x3 en función de x4, que se tomará como parámetro del sistema.
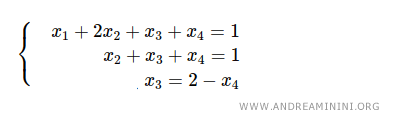
Luego se sustituye x3 = 2 - x4 en la segunda ecuación, obteniendo x2 = -1.
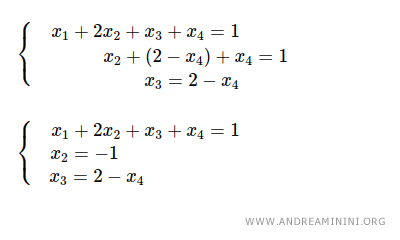
Finalmente, se sustituyen x2 = -1 y x3 = 2 - x4 en la primera ecuación, obteniendo x1 = 1.
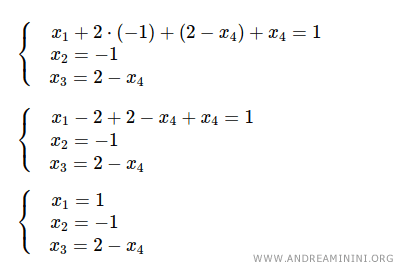
Las soluciones del sistema son: x1 = 1, x2 = -1, x3 = 2 - x4, considerando x4 como parámetro libre k ∈ ℝ.
$$ \begin{cases} x_1 = 1 \\ x_2 = -1 \\ x_3 = 2 - k \end{cases} $$
Por tanto, el sistema admite infinitas soluciones.
Observaciones
Algunas observaciones útiles sobre los sistemas lineales escalonados:
- Todas las matrices escalonadas son matrices triangulares superiores. Sin embargo, no todas las matrices triangulares superiores son matrices escalonadas.
- El determinante de una matriz cuadrada escalonada es igual al producto de los elementos de su diagonal principal. Al tratarse de una matriz triangular, basta con multiplicar los elementos de la diagonal principal, ya que el resto de los elementos son nulos. Por ello, el cálculo del determinante en matrices escalonadas es especialmente sencillo.
Y así sucesivamente.