Vectores paralelos
Dos vectores en un plano se denominan paralelos cuando son linealmente dependientes.
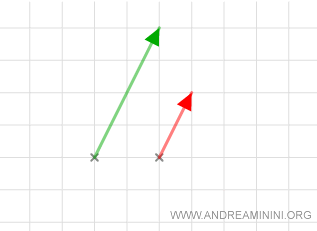
Ejemplo práctico
Consideremos dos vectores \( v_1 \) y \( v_2 \) en el espacio vectorial \( V = \mathbb{R}^2 \), definido sobre el cuerpo \( K = \mathbb{R} \):
$$ v_1 = \overrightarrow{AB} = (2, 4) \\ v_2 = \overrightarrow{CD} = (1, 2) $$
Estos dos vectores son linealmente dependientes si el determinante de la matriz formada por los dos vectores columna es igual a cero:
$$ det \begin{pmatrix} 2 & 1 \\ 4 & 2 \end{pmatrix} = 0 $$
Esto implica que los dos vectores son proporcionales.
Nota: En este caso, el vector \( \overrightarrow{AB} \) es el doble del vector \( \overrightarrow{CD} \): $$ \overrightarrow{CD} = 2 \cdot \overrightarrow{AB} = 2 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
El rango de la matriz de los vectores columna es como máximo uno:
$$ rg \begin{pmatrix} 2 & 1 \\ 4 & 2 \end{pmatrix} \le 1 $$
Demostración
Representemos gráficamente ambos vectores con origen en \( O(0,0) \):
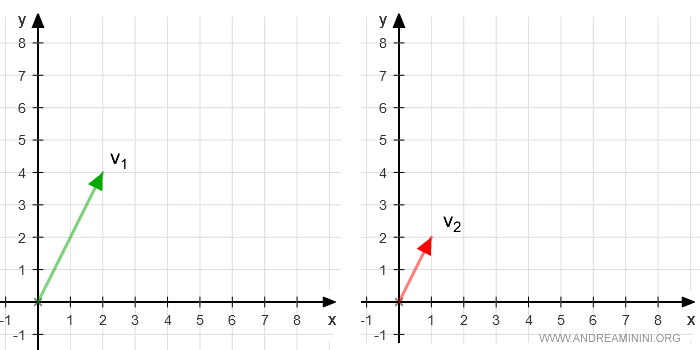
Resulta evidente que los dos vectores son proporcionales, ya que se encuentran sobre la misma recta que pasa por el origen.
Uno de los vectores es un múltiplo del otro. Existe un escalar \( k \) tal que \( v_1 = k \cdot v_2 \).
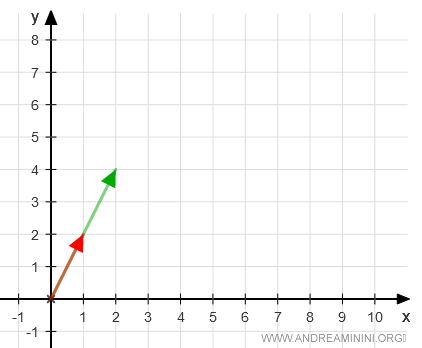
Esto demuestra la dependencia lineal de ambos vectores.
Y así sucesivamente.
Corolarios
- Vector paralelo a una recta
Un vector es paralelo a una recta \( r \) en el plano si pertenece a una recta paralela a \( r \), o bien a la propia recta \( r \).
- Vector aplicado en un punto
Todo punto \( P \) en el plano define un vector aplicado \( \overrightarrow{PP} \) que es paralelo a cualquier recta del plano.
Vectores paralelos en el espacio
En un espacio tridimensional \( \mathbb{R}^3 \):
Un vector es paralelo a una recta si comparte el mismo vector director o es proporcional a dicho vector.
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \\ n \end{pmatrix} $$
Donde \( (l, m, n) \) es el vector director de la ecuación vectorial de la recta, y \( (x_0, y_0, z_0) \) es un punto cualquiera sobre ella.
El vector director determina la dirección de todas las rectas paralelas al propio vector.
Un vector es paralelo a un plano si pertenece a un plano paralelo a este.