Distancia entre vectores
La distancia vectorial es una medida que cuantifica cuán alejados se encuentran dos vectores en el espacio. Se calcula habitualmente a partir de la norma de su diferencia: \[ d(\vec{v}, \vec{w}) = |\vec{v} - \vec{w}| \]
Imagina dos puntos en un espacio tridimensional - aunque este razonamiento es válido en espacios de cualquier dimensión.
Supongamos que uno de los puntos se encuentra en \(\vec{v} = (x_1, y_1, z_1)\) y el otro en \(\vec{w} = (x_2, y_2, z_2)\).
La distancia entre ambos corresponde al módulo (o norma) del vector diferencia \(\vec{v} - \vec{w}\):
\[ |\vec{v} - \vec{w}| = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2} \]
Esta fórmula es una extensión directa del teorema de Pitágoras al espacio tridimensional.
Nota. Cuando hablamos de la distancia entre vectores, normalmente nos referimos a la norma euclídea, es decir, la raíz cuadrada de la suma de los cuadrados de las diferencias. No obstante, en ciertos contextos se emplean otras normas. Por ejemplo, la distancia Manhattan (también conocida como distancia en retícula o norma L1) se expresa como \(|x_1 - x_2| + |y_1 - y_2| \), mientras que la distancia de Chebyshev (o norma L∞) corresponde a \(\max(|x_1 - x_2|, |y_1 - y_2|)\).
Ejemplo resuelto
Consideremos dos vectores en \(\mathbb{R}^2\):
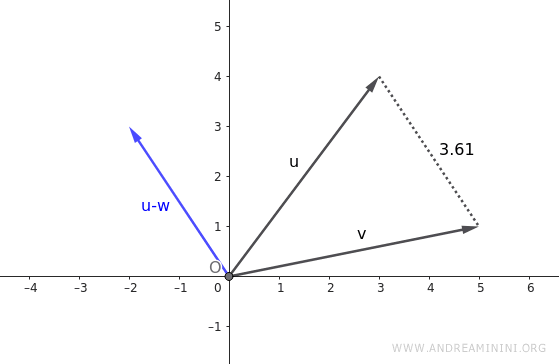
\[ \vec{v} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} \]
\[ \vec{w} = \begin{pmatrix} 5 \\ 1 \end{pmatrix} \]
Empezamos calculando su diferencia:
\[ \vec{v} - \vec{w} = \begin{pmatrix} 3 - 5 \\ 4 - 1 \end{pmatrix} = \begin{pmatrix} -2 \\ 3 \end{pmatrix} \]
El módulo del vector diferencia resultante es:
\[ |\vec{v} - \vec{w}| = \sqrt{(-2)^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13} \]
Por lo tanto, la distancia entre los dos vectores es \(\sqrt{13}\), lo que equivale aproximadamente a 3,6 unidades.
Distancia en espacios de dimensión superior
La misma fórmula se aplica en espacios de cualquier dimensión.
Por ejemplo, consideremos dos vectores en un espacio de cuatro dimensiones \(\mathbb{R}^4\):
\[ \vec{a} = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} \]
\[ \vec{b} = \begin{pmatrix} 3 \\ 0 \\ -1 \\ 2 \end{pmatrix} \]
La diferencia entre ambos es:
\[ \vec{a} - \vec{b} = \begin{pmatrix} -2 \\ 2 \\ 4 \\ 2 \end{pmatrix} \]
Y la distancia euclídea resulta ser:
\[ |\vec{a} - \vec{b}| = \sqrt{(-2)^2 + 2^2 + 4^2 + 2^2} = \sqrt{4 + 4 + 16 + 4} = \sqrt{28} \approx 5,29 \]
Nota. En espacios de alta dimensión, la distancia vectorial es un concepto fundamental en informática. Se emplea de forma habitual para medir la similitud entre puntos de datos - como imágenes, documentos de texto o perfiles de usuario - y desempeña un papel crucial en áreas como los gráficos 3D, el reconocimiento de patrones y los algoritmos de aprendizaje automático, tales como k vecinos más cercanos (k-NN) y los métodos de agrupamiento (clustering).
Y así sucesivamente.