Multiplicación escalar de un vector

Cuando multiplico un vector v por un escalar, denotado como k, estoy escalando cada uno de sus componentes por dicho escalar. Esta operación se representa de la siguiente forma:

$$ k \cdot \vec{v} = k \cdot \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} = \begin{pmatrix} k \cdot v_1 \\ k \cdot v_2 \\ \vdots \\ k \cdot v_n \end{pmatrix} $$

En este contexto, un "escalar" es simplemente un número real.

Multiplicar un vector v por un escalar k genera un nuevo vector w = k · v que:

Apunta en la misma dirección que v si k es positivo.
Tiene una magnitud igual a |k| veces la magnitud de v.
Cambia de sentido si k es negativo.

Nota: Si k = 0, el resultado es el vector nulo, es decir, el vector v queda "anulado". Si k = 1, el vector permanece inalterado; si k = -1, el vector se invierte y obtenemos -v.

Ejemplo práctico

Consideremos un vector v en el espacio tridimensional (x, y, z):

$$ \vec{v} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} $$

Multiplicando este vector por un escalar k = 2 obtenemos:

$$ k \cdot \vec{v} = 2 \cdot \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} $$

El vector resultante es:

$$ k \cdot \vec{v} = 2 \cdot \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} = \begin{pmatrix} 6 \\ 2 \\ -4 \end{pmatrix} $$

Ejemplo 2

Si tenemos un vector v con magnitud |v| = 3 y un escalar k = 2:

ejemplo de multiplicación escalar de un vector en el plano

El vector resultante w mantiene la misma dirección que v, pero su magnitud es 6:

$$ \vec{w} = |k| \cdot \vec{v} $$

$$ | \vec{w} | = |k| \cdot | \vec{v} | = 2 \cdot 3 = 6 $$

Esta relación se ilustra visualmente a continuación.

representación gráfica del aumento de magnitud tras la multiplicación escalar

Nota: Multiplicar un vector por un escalar k implica escalar cada uno de sus componentes. Por ejemplo, si k = 3 y v = (1,2)^T:

$$ k \cdot \vec{v} = 3 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 3 \\ 6 \end{pmatrix} $$

Esta transformación también puede representarse gráficamente.
visualización gráfica del escalado de un vector mediante multiplicación escalar

Ejemplo 3

Si tenemos un vector v con magnitud |v| = 3 y un escalar negativo k = -2:

ejemplo de cambio de dirección con multiplicación escalar negativa

El vector resultante w apunta en sentido opuesto a v y su magnitud es 6:

$$ | \vec{w} | = |k| \cdot | \vec{v} | = |-2| \cdot 3 = 6 $$

Este cambio tanto en la dirección como en la magnitud también se puede visualizar de la siguiente manera.

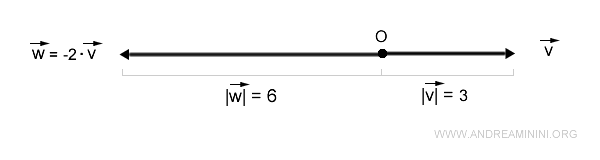
representación gráfica del cambio de dirección mediante multiplicación escalar negativa

Nota: Cuando k = -1, el resultado es -v, un vector con la misma magnitud que v, pero orientado en sentido contrario.