Vector opuesto

El vector opuesto de $ \vec{v} $ es un vector $ -\vec{v} $ que presenta la misma dirección y magnitud (longitud), pero cuyo sentido es contrario al de \( \vec{v} \).

Para obtener el vector opuesto, basta con multiplicar el vector \( \vec{v} \) por el escalar -1 mediante la operación de multiplicación por un escalar.

Un ejemplo práctico

Consideremos un vector cuya magnitud es igual a 3.

La recta sobre la que se apoya el vector determina su dirección, mientras que su longitud (magnitud) es 3.

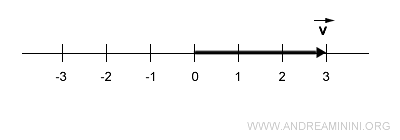
El vector opuesto es otro vector situado sobre la misma recta (misma dirección), con igual longitud (3), pero orientado en el sentido contrario.

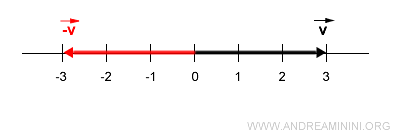
Ejemplo 2

Consideremos ahora un vector en un espacio bidimensional:

$$ \vec{v} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

En un sistema de coordenadas cartesianas, este vector conecta el origen \( O \) con el punto de coordenadas \( (1,2) \).

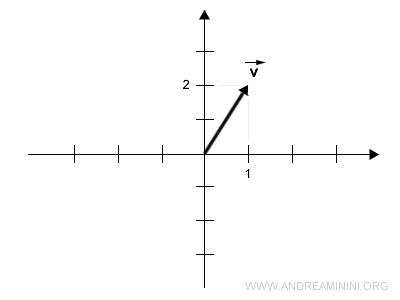
Para calcular el vector opuesto, multiplicamos el vector \( \vec{v} \) por el escalar -1:

$$ - \vec{v} = -1 \cdot \vec{v} $$

$$ - \vec{v} = -1 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

$$ - \vec{v} = \begin{pmatrix} -1 \cdot 1 \\ -1 \cdot 2 \end{pmatrix} $$

$$ - \vec{v} = \begin{pmatrix} -1 \\ -2 \end{pmatrix} $$

El vector opuesto conecta el origen con el punto de coordenadas \( (-1,-2) \).

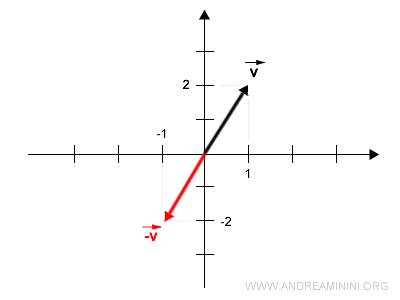
Observaciones adicionales

Algunas consideraciones y propiedades relevantes sobre los vectores opuestos:

• La suma de un vector y su opuesto siempre da como resultado el vector nulo
  Sea \( \vec{v} \) un vector en un espacio vectorial \( V \). Su vector opuesto, denotado como \( -\vec{v} \), es el único vector que, al sumarse con \( \vec{v} \), produce el vector nulo. $$ \vec{v} + (-\vec{v}) = \vec{0} $$ Esta propiedad se deduce directamente de la definición del vector opuesto y de las propiedades asociativa y conmutativa de la suma vectorial.

  Ejemplo. Consideremos el vector \( \vec{v} \) en el espacio vectorial \( \mathbb{R}^2 \): $$ \vec{v} = \begin{pmatrix} 3 \\ -2 \end{pmatrix} $$ Su vector opuesto es: $$ -\vec{v} = \begin{pmatrix} -3 \\ 2 \end{pmatrix} $$ Ahora sumamos \( \vec{v} \) y \( -\vec{v} \): $$ \vec{v} + (-\vec{v}) = \begin{pmatrix} 3 \\ -2 \end{pmatrix} + \begin{pmatrix} -3 \\ 2 \end{pmatrix} = \begin{pmatrix} 3 - 3 \\ -2 + 2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$ El resultado es el vector nulo: \( \vec{0} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \).

Y así sucesivamente.