Resta de vectores
Al trabajar con vectores, resulta fundamental comprender el concepto de resta. Analicémoslo en detalle.
Dados dos vectores, v y w, con el mismo número de componentes, la operación v-w consiste en restar, componente a componente, las coordenadas de w a las de v. Matemáticamente: $$ \vec{v} - \vec{w} = \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} - \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{pmatrix} = \begin{pmatrix} v_1 - w_1 \\ v_2 - w_2 \\ \vdots \\ v_n - w_n \end{pmatrix} $$ El resultado es el vector diferencia.
Es importante señalar que la resta de vectores solo es válida cuando ambos poseen el mismo número de componentes. En caso contrario, la operación no está definida.
Ejemplo
Veamos un ejemplo concreto.
Consideremos los siguientes vectores:
$$ \vec{v} = \begin{pmatrix} 2 \\ 5 \end{pmatrix} $$
$$ \vec{w} = \begin{pmatrix} 4 \\ 3 \end{pmatrix} $$
En esta operación, v actúa como minuendo y w como sustraendo.
$$ \vec{v} - \vec{w} $$
Restamos las componentes correspondientes de v y w:
$$ \vec{v} - \vec{w} = \begin{pmatrix} 2 \\ 5 \end{pmatrix} - \begin{pmatrix} 4 \\ 3 \end{pmatrix} = \begin{pmatrix} 2-4 \\ 5-3 \end{pmatrix} = \begin{pmatrix} -2 \\ 2 \end{pmatrix} $$
Este es el vector diferencia resultante.
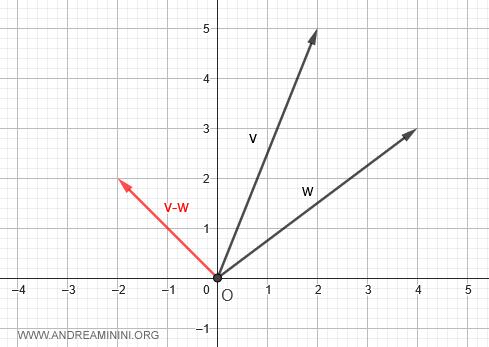
Método gráfico
Para quienes prefieren una interpretación visual, exploraremos el método gráfico:
Partimos de los vectores:
$$ \vec{v} = \begin{pmatrix} 2 \\ 5 \end{pmatrix} $$
$$ \vec{w} = \begin{pmatrix} 4 \\ 3 \end{pmatrix} $$
Representamos ambos vectores en un sistema de coordenadas cartesianas.
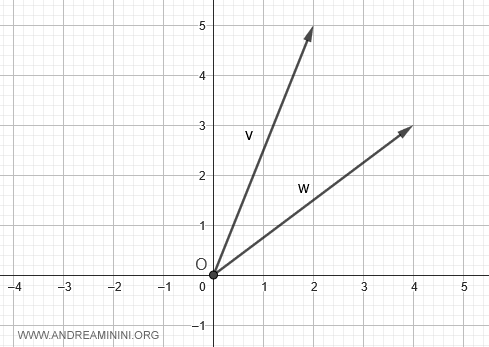
Para efectuar la resta:
$$ \vec{v} - \vec{w} $$
En la representación gráfica, comenzamos en el punto donde se aplica el vector sustraendo w, es decir, el punto A con coordenadas (4,3).
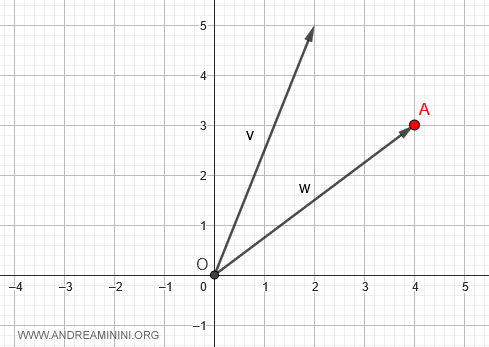
Desde allí, aplicamos el vector opuesto -w, desplazándonos en dirección al origen (O).
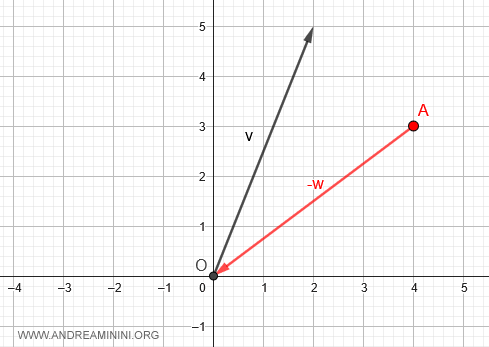
A continuación, aplicamos el vector minuendo v, que nos lleva hasta el punto B con coordenadas (2,5).
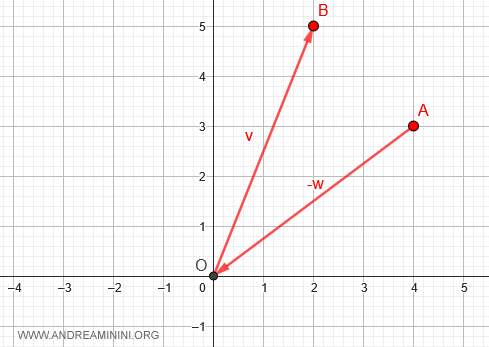
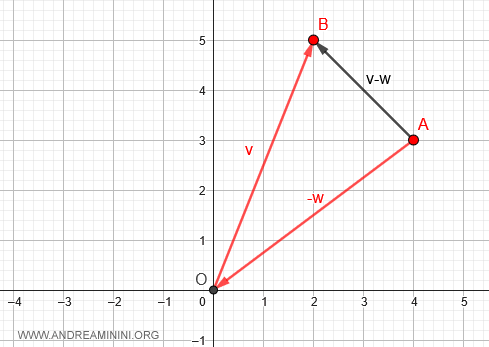
Al unir los puntos A y B mediante un segmento dirigido, obtenemos el vector desplazamiento.
En física, este segmento se conoce como vector desplazamiento, pues representa el cambio de posición entre dos puntos.
Finalmente, trasladamos la base del vector desplazamiento al origen (O).
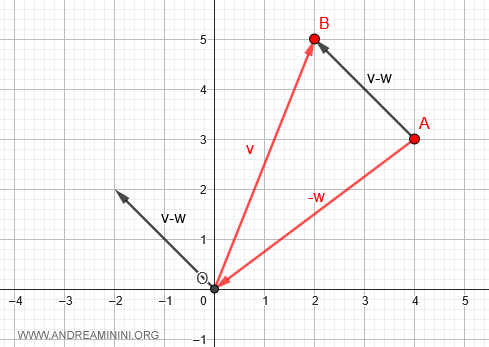
El vector resultante representa la diferencia entre v y w.
Espero que esta explicación te haya ayudado a comprender con mayor claridad el concepto de resta de vectores.