Descomposición de un vector

Cuando hablamos de descomponer un vector, nos referimos a expresarlo en términos de sus componentes a lo largo de los ejes cartesianos. Es decir, un vector \( \vec{v} \) puede representarse como la suma de sus componentes \( \vec{v_x} \), \( \vec{v_y} \) y \( \vec{v_z} \): $$ \vec{v} = \vec{v_x} + \vec{v_y} + \vec{v_z} $$ También puede escribirse como una combinación lineal de los vectores unitarios: $$ \vec{v} = \alpha_1 \vec{u_x} + \alpha_2 \vec{u_y} + \alpha_3 \vec{u_z} $$

Aquí, los vectores unitarios u_x, u_y, u_z representan las direcciones estándar en un sistema de coordenadas cartesianas tridimensional (x, y, z).

Los escalares α₁, α₂, α₃ son valores concretos que determinan la descomposición del vector.

¿Qué son exactamente estos componentes vectoriales? Son las proyecciones del vector sobre los ejes cartesianos. Por ejemplo, consideremos los componentes \( \vec{v_x} \) y \( \vec{v_y} \) de un vector \( \vec{v} \) en un plano cartesiano bidimensional (x, y).

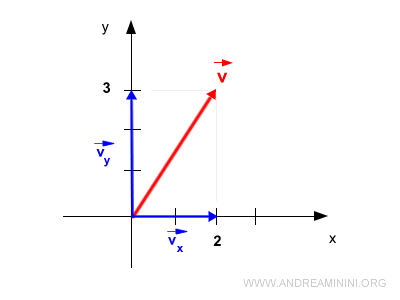
Cabe destacar que estos componentes son a su vez vectores, no simples escalares.

Ejemplo práctico

Consideremos un vector bidimensional v=(2,3)^T, que podemos representar así:

$$ \vec{v} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

A continuación, su representación gráfica.

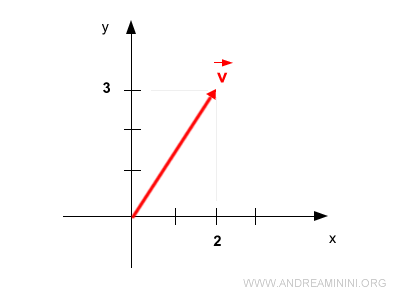
Al proyectar \( \vec{v} \) sobre el eje x, obtenemos su componente en x.

 

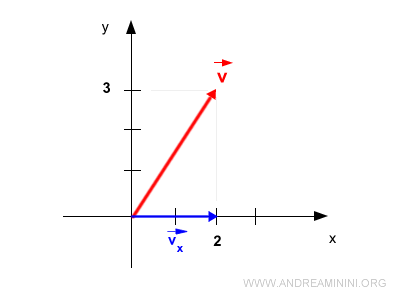
De igual manera, al proyectarlo sobre el eje y obtenemos su componente en y.

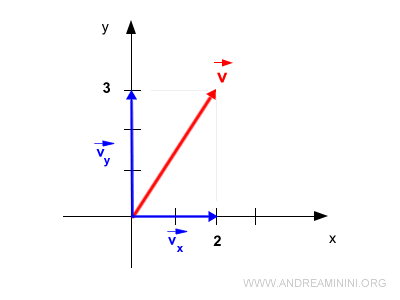
Tanto \( \vec{v_x} \) como \( \vec{v_y} \) son vectores.

Por tanto, las componentes en ambas direcciones son:

$$ \vec{v_x} = \begin{pmatrix} 2 \\ 0 \end{pmatrix} $$

$$ \vec{v_y} = \begin{pmatrix} 0 \\ 3 \end{pmatrix} $$

La suma vectorial de \( \vec{v_x} \) y \( \vec{v_y} \) nos devuelve el vector original \( \vec{v} \).

$$ \vec{v_x} + \vec{v_y} = \begin{pmatrix} 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 3 \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} = \vec{v} $$

Podemos expresar los componentes \( \vec{v_x} \) y \( \vec{v_y} \) como el producto del vector unitario correspondiente por un escalar.

$$ \vec{v_x} = x \cdot \vec{u_x} $$

$$ \vec{v_y} = y \cdot \vec{u_y} $$

Por ejemplo, con las coordenadas x=2 e y=3:

$$ \vec{v_x} = 2 \cdot \vec{u_x} $$

$$ \vec{v_y} = 3 \cdot \vec{u_y} $$

Como los vectores unitarios en un sistema cartesiano son \( \vec{u_x} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \) y \( \vec{u_y} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \), podemos escribir la suma de los componentes así:

$$ \vec{v_x} + \vec{v_y} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 3 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

La suma de los componentes equivale al vector \( \vec{v} \).

$$ \vec{v} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 3 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

Esta combinación lineal de vectores unitarios y escalares nos permite reconstruir el vector original \( \vec{v} \).

$$ \vec{v} = \vec{v_x} + \vec{v_y} $$

$$ \vec{v} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 3 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

$$ \vec{v} = \begin{pmatrix} 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 3 \end{pmatrix} $$

$$ \vec{v} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

Nota. Los módulos de los componentes \( \vec{v_x} \) y \( \vec{v_y} \) también pueden calcularse mediante funciones trigonométricas: $$ | \vec{v_x} | = r \cdot \sin \Phi $$ $$ | \vec{v_y} | = r \cdot \cos \Phi $$ donde \( \Phi \) es el ángulo que forma el vector con el eje x, y r es el módulo del vector.

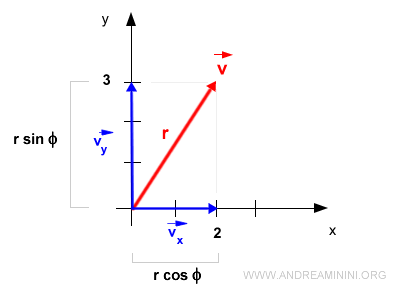
El módulo del vector puede calcularse aplicando el teorema de Pitágoras: $$ r = \sqrt{ |\vec{x}|^2 + |\vec{y}|^2 } $$ $$ r = \sqrt{ 2^2 + 3^2 } $$ $$ r = \sqrt{ 4 + 9 } $$ $$ r = \sqrt{ 13 } $$

Ejemplo 2

Si el vector se encuentra en una posición distinta del origen, será necesario calcular su proyección tanto en el punto de origen como en el extremo del vector.

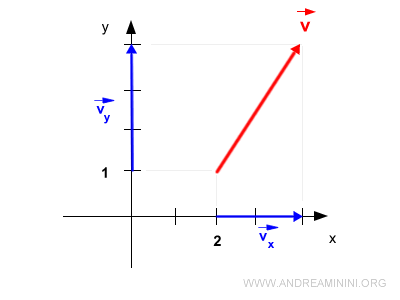
Y así sucesivamente.