Flujo de un campo vectorial
¿Qué es el flujo de un campo vectorial?
El flujo de un campo vectorial V a través de una superficie S en el espacio es una magnitud escalar definida como la integral de superficie del producto escalar v·ds, evaluada punto a punto sobre S: $$ Φ_S = \int_S \vec{v} \cdot \vec{ds} $$
Aquí, $\vec{v}$ representa los vectores del campo V, mientras que $\vec{ds}$ son vectores normales infinitesimales orientados hacia el exterior y perpendiculares a cada elemento diferencial de superficie de S.
El producto escalar $\vec{v} \cdot \vec{ds}$ en cada punto s de la superficie se denomina contribución local al flujo.
$$ \vec{v} \cdot \vec{ds} $$
La suma de todas estas contribuciones locales a lo largo de toda la superficie S define el flujo total del campo vectorial a través de S:
$$ Φ_S = \int_S \vec{v} \cdot \vec{ds} $$
Nota: La superficie S puede ser abierta o cerrada. En una superficie abierta, la orientación del vector normal puede elegirse libremente; se considera que el flujo es positivo si se dirige hacia el exterior, y negativo si apunta hacia el interior. En una superficie cerrada, por convención, los vectores normales se orientan hacia el exterior. El flujo a través de una superficie cerrada se representa mediante una integral de superficie con un círculo: $$ Φ_S = \oint_S \vec{v} \cdot \vec{ds} $$
Un ejemplo práctico
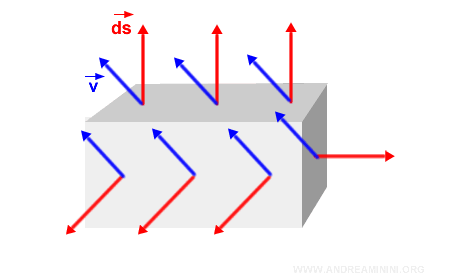
Consideremos una superficie cerrada y curva S.

Dividimos la superficie en elementos infinitesimales s.
De este modo, podemos considerar cada pequeño elemento como un parche plano a nivel local.
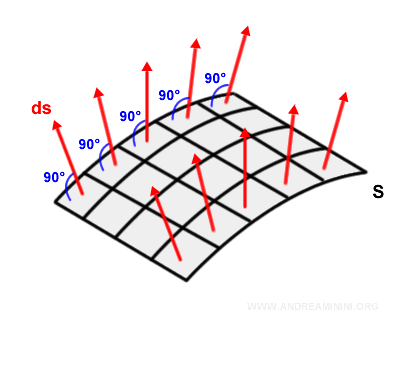
En cada punto s se dibuja el vector normal orientado hacia el exterior $\vec{ds}$, cuya magnitud corresponde al área del elemento diferencial de superficie asociado.
Un vector normal es perpendicular al plano tangente local; es decir, forma un ángulo de 90° con la superficie en ese punto.
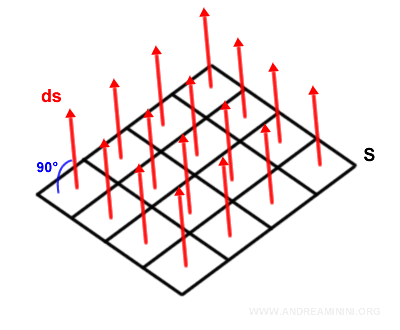
Nota: Si la superficie S fuera plana, todos los vectores normales apuntarían en la misma dirección. El principio fundamental permanece inalterado.
A continuación, introducimos un campo vectorial V - por ejemplo, un campo eléctrico o un campo magnético.
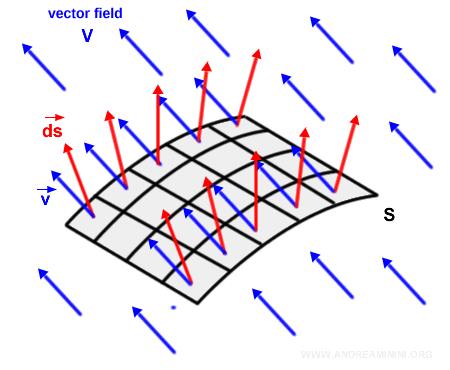
Nota: Para mayor claridad, en la ilustración se muestra un campo vectorial constante, en el que todos los vectores presentan la misma dirección, magnitud y orientación. El mismo razonamiento se aplica a campos más generales, con direcciones, magnitudes y orientaciones variables.
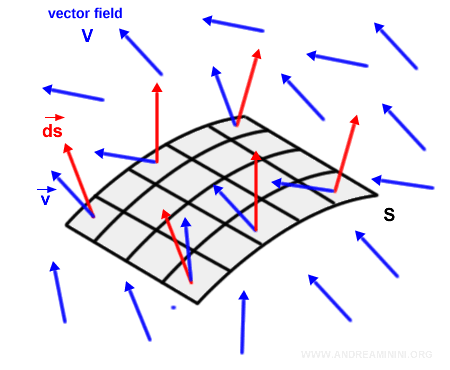
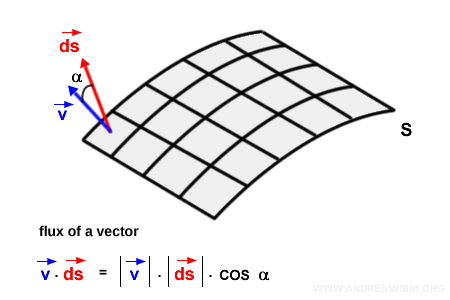
Para cada elemento de superficie s, calculamos el producto escalar entre el vector del campo $\vec{v}$ y el vector normal $\vec{ds}$.
El producto escalar de dos vectores equivale al producto de sus magnitudes $|\vec{v}| \cdot |\vec{ds}|$ multiplicado por el coseno del ángulo $\alpha$ que forman:
$$ \vec{v} \cdot \vec{ds} = |\vec{v}| \cdot |\vec{ds}| \cdot \cos \alpha $$
La contribución al flujo en cada elemento diferencial de superficie s es este producto escalar local.
Este proceso se repite para cada elemento diferencial de superficie $\vec{ds}$.
El valor de $\vec{v} \cdot \vec{ds}$ varía de un punto a otro, ya que el ángulo entre el vector del campo y el vector normal cambia a lo largo de la superficie.
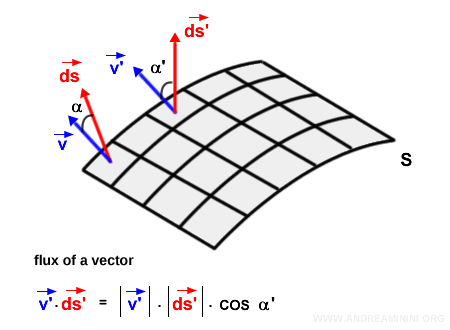
Nota: En campos vectoriales más complejos, tanto la dirección como la magnitud de los vectores pueden variar. Estas variaciones influyen adicionalmente en el valor del producto escalar en cada punto.
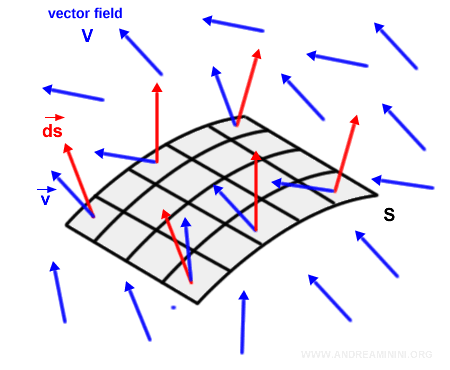
La suma de todas las contribuciones al flujo sobre la superficie S da lugar al flujo total del campo vectorial.
Como se trata de una suma sobre elementos infinitesimales, se expresa mediante una integral:
$$ Φ_S = \int_S \vec{v} \cdot \vec{ds} $$
Nota: Si S encierra un sólido, el flujo del campo vectorial debe calcularse para cada cara de la superficie que delimita dicho sólido. El procedimiento es el mismo en cada caso. Por ejemplo, si el sólido es un cubo o un paralelepípedo rectangular, se calcula el flujo en cada una de sus seis caras de manera individual.
Y así sucesivamente.