Vectores Unitarios
¿Qué es un vector unitario?
Un vector unitario es un vector cuya magnitud (o módulo) es exactamente 1 y que indica una dirección determinada en el espacio.
Sobre una misma dirección (una recta), existen infinitos vectores con diferentes longitudes, orientados en uno u otro sentido a lo largo de esa línea.
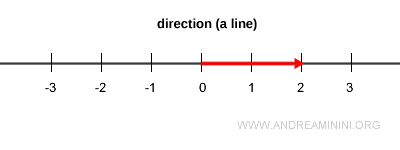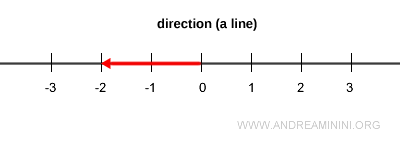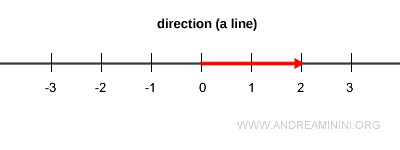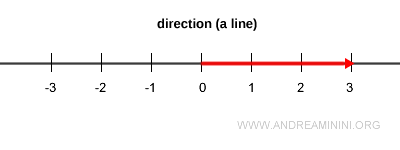
No obstante, en cada dirección existe un único vector cuya longitud es exactamente uno: ese es el vector unitario.
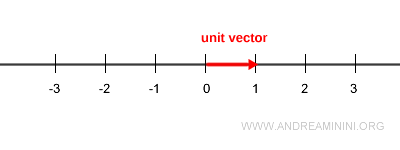
¿Por qué se llama vector unitario?
Se denomina “unitario” porque su módulo es igual a uno. Este tipo de vector sirve para definir una dirección y un sentido a lo largo de una línea recta.
¿Para qué se utilizan los vectores unitarios?
Cualquier vector con la misma dirección puede obtenerse multiplicando el vector unitario por un número real \( k \).
Ejemplo
Sea \( \vec{v} \) un vector unitario.
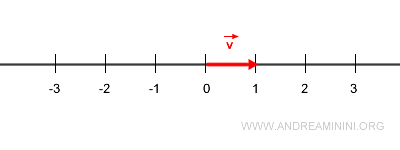
Supongamos que \( \vec{w} \) es un vector de módulo 3.
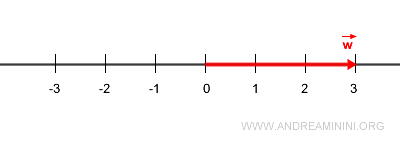
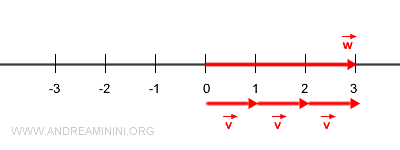
Entonces, \( \vec{w} \) puede expresarse como el producto escalar de \( \vec{v} \) por 3:
$$ \vec{w} = 3 \cdot \vec{v} $$
El resultado es un vector con la misma dirección que \( \vec{v} \), pero tres veces más largo.
Ejemplo 2
De nuevo, sea \( \vec{v} \) un vector unitario.
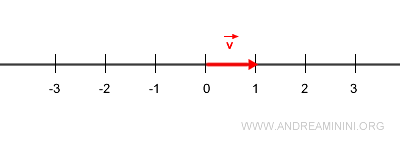
Ahora consideremos un vector \( \vec{u} \) de módulo 2, pero orientado en sentido contrario.
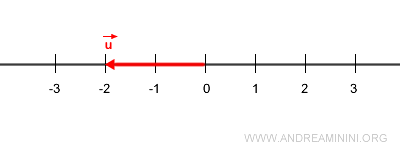
Nota. El módulo de \( \vec{u} \) es 2. No tendría sentido decir que su magnitud es -2: el módulo de un vector siempre es positivo. El signo negativo solo indica el sentido relativo respecto al vector unitario.
El vector \( \vec{u} \) se obtiene multiplicando \( \vec{v} \) por -2:
$$ \vec{w} = -2 \cdot \vec{v} $$
El escalar negativo invierte la dirección del vector:
$$ \vec{w} = 2 \cdot (-\vec{v}) $$
En este caso, \( -\vec{v} \) es el vector opuesto de \( \vec{v} \).
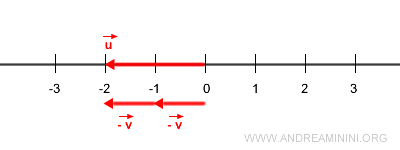
En definitiva, una vez conocido el vector unitario, es posible generar cualquier vector sobre esa misma recta mediante multiplicación escalar.
Vectores Unitarios en los Ejes Coordenados
Cualquier vector en el espacio cartesiano tridimensional puede escribirse como una combinación lineal de los vectores unitarios que apuntan en las direcciones de los ejes \( x \), \( y \) y \( z \): $$ \vec{w} = \alpha_1 \cdot \vec{u_x} + \alpha_2 \cdot \vec{u_y} + \alpha_3 \cdot \vec{u_z} $$
Estos vectores unitarios se suelen denotar como \( \vec{u_x} \), \( \vec{u_y} \), y \( \vec{u_z} \), o bien mediante las notaciones estándar \( \hat{i} \), \( \hat{j} \) y \( \hat{k} \).
Los coeficientes \( \alpha_1 \), \( \alpha_2 \) y \( \alpha_3 \) son escalares, es decir, números reales que determinan la proyección del vector sobre cada eje.
Ejemplo
En dos dimensiones, basta con considerar los vectores \( \vec{u_x} \) y \( \vec{u_y} \).
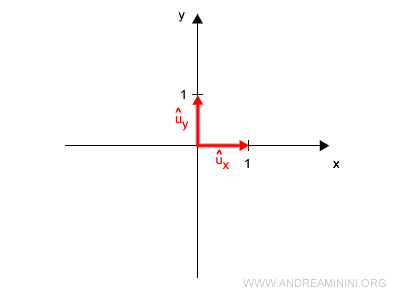
Nota. Para mayor claridad, usamos los vectores unitarios de la base canónica: $$ \vec{u_x} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \quad \vec{u_y} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$ Naturalmente, cualquier par de vectores linealmente independientes también puede formar una base del plano.
La combinación lineal de estos vectores permite expresar cualquier vector bidimensional.
Por ejemplo, para construir el vector \( \vec{w} = (2,1)^T \):
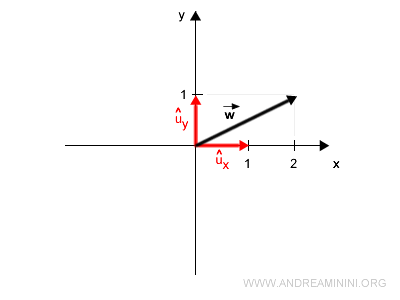
Nota. El superíndice \( T \) indica la transposición, es decir, que el vector fila se convierte en un vector columna: $$ \vec{w} = \begin{pmatrix} 2 , 1 \end{pmatrix}^T = \begin{pmatrix} 2 \\ 1 \end{pmatrix} $$
De este modo, el vector se puede escribir como:
$$ \vec{w} = \alpha_1 \cdot \vec{u_x} + \alpha_2 \cdot \vec{u_y} $$
donde \( \alpha_1 = 2 \) y \( \alpha_2 = 1 \):
$$ \vec{w} = 2 \cdot \vec{u_x} + 1 \cdot \vec{u_y} $$
Sustituyendo los vectores unitarios en su forma matricial:
$$ \vec{w} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 1 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$
Realizando las multiplicaciones escalares:
$$ \vec{w} = \begin{pmatrix} 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$
Y sumando los vectores componente a componente:
$$ \vec{w} = \begin{pmatrix} 2+0 \\ 0+1 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} $$
Así, cualquier vector en el espacio cartesiano puede expresarse como combinación lineal de los vectores unitarios de la base.
Y así sucesivamente.