Suma de dos vectores

Al trabajar con dos vectores, por ejemplo v y w, podemos calcular su suma v+w de distintas maneras. Una de las más habituales es el método del paralelogramo. Otra consiste en sumar directamente las coordenadas de ambos vectores. De forma matemática: $$ \vec{v} + \vec{w} = \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} + \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{pmatrix} = \begin{pmatrix} v_1 + w_1 \\ v_2 + w_2 \\ \vdots \\ v_n + w_n \end{pmatrix} $$

Sea cual sea el procedimiento elegido, el resultado es siempre el mismo: la suma de v y w genera un nuevo vector.

Este nuevo vector recibe el nombre de 'vector suma'.

Método del paralelogramo

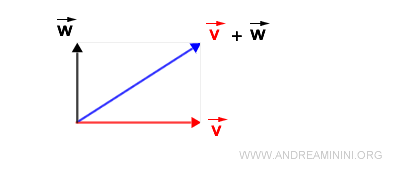
Cuando representamos los vectores en el plano, el método del paralelogramo ofrece una interpretación geométrica muy intuitiva de su suma.

Consideremos dos vectores, v y w. Ambos parten de un mismo punto, O, pero apuntan en direcciones distintas.

• El vector v se extiende desde el punto O hasta el punto A, representando su módulo.
• El vector w va desde el punto O hasta el punto B.

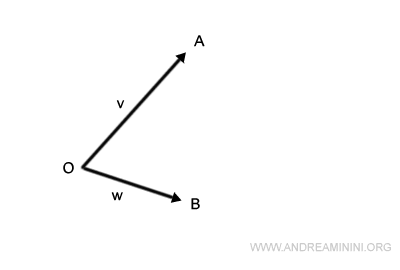
¿Cómo podemos entonces determinar su suma?

En primer lugar, trasladamos el segmento OA de modo que su origen pase al punto B.

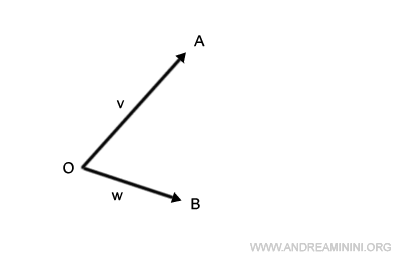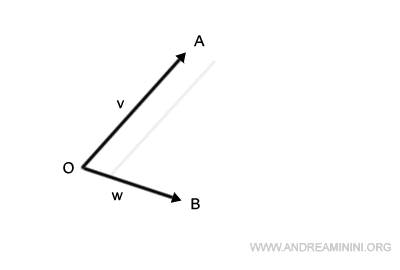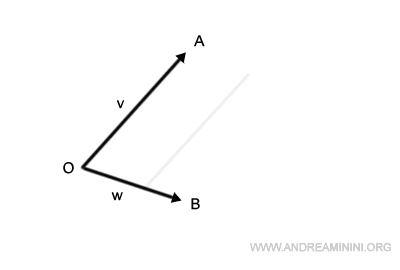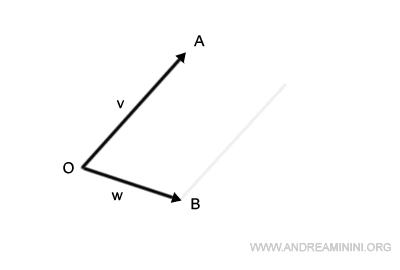
De forma análoga, desplazamos el segmento OB para que comience en el punto A.

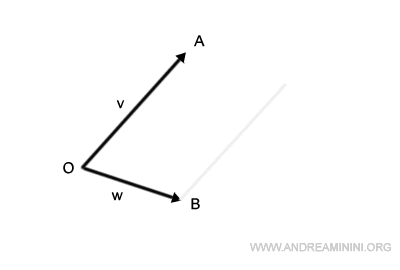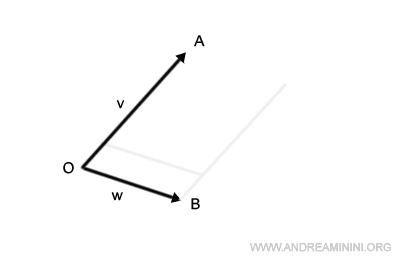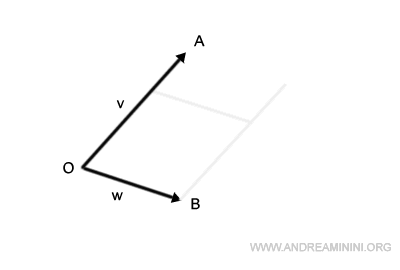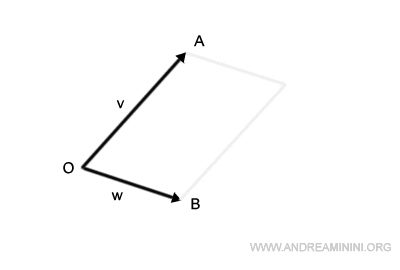
El punto de intersección de estos segmentos desplazados es el punto C.

Así queda definido el paralelogramo OACB.

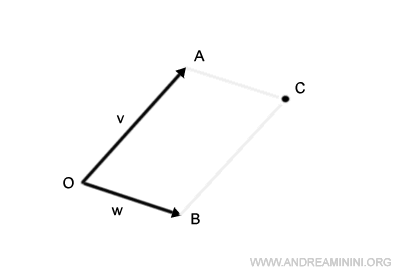
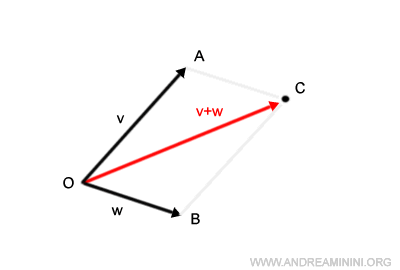
El segmento que une el origen, O, con el punto C representa la suma de los vectores v+w.

Si los dos vectores tienen la misma dirección, sus longitudes quedan alineadas en una única recta. En este caso, el método del paralelogramo no es aplicable, ya que daría lugar a una figura degenerada. Por ello, en estas situaciones se emplea habitualmente el método del punto medio.

Cálculo vectorial: un ejemplo

En el espacio vectorial V=R², consideremos dos vectores concretos:

$$ P_1 \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$ $$ P_2 \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \end{pmatrix}$$

Estos vectores se representan en el plano cartesiano (x,y) como segmentos dirigidos: OP₁ y OP₂, que van desde el origen hasta los puntos P₁ y P₂, respectivamente.

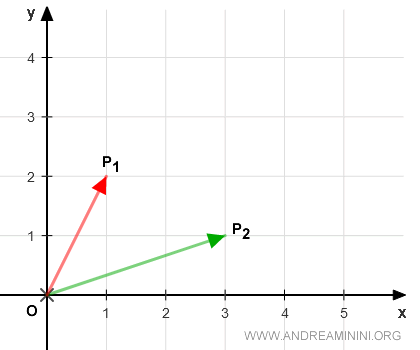
Es importante comprender que cualquier punto del plano puede asociarse a un vector que parte del origen. De forma recíproca, todo vector con origen en O corresponde a un punto concreto en el plano (x,y). En otras palabras, puntos y vectores constituyen dos formas equivalentes de describir la misma realidad geométrica.

Para calcular la suma de los vectores OP1 y OP₂, empleamos el método del paralelogramo.

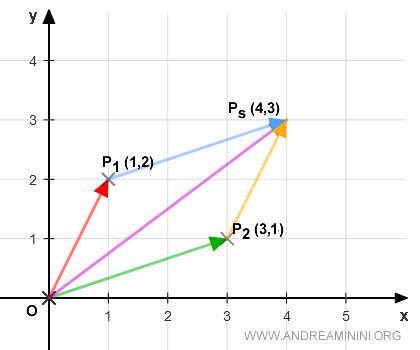
El vector resultante, OP₁+OP₂, conecta el origen con el punto P_s(4,3).

Método punta-cola

Existe un procedimiento especialmente intuitivo para sumar vectores: el método punta-cola. En lugar de recurrir a cálculos algebraicos, basta con trasladar un vector para que su base coincida con la punta (extremo) de otro.

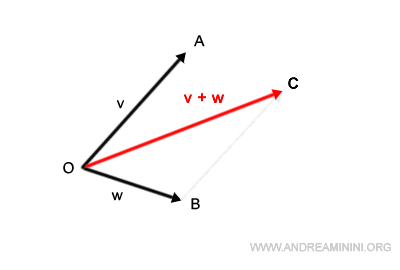
Este método permite identificar de forma sencilla el vector resultante v+w.

Ejemplo práctico:

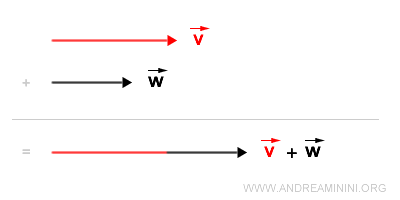
Supongamos que queremos sumar los vectores v y w. Procedemos así:

Desplazamos la base del vector v para que coincida con la punta del vector w.

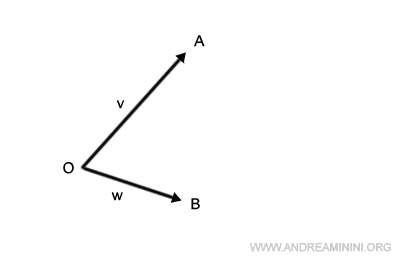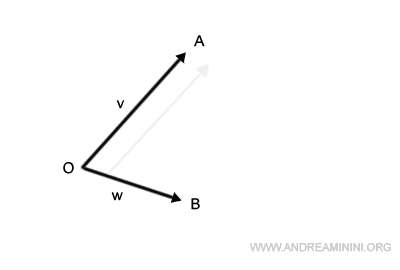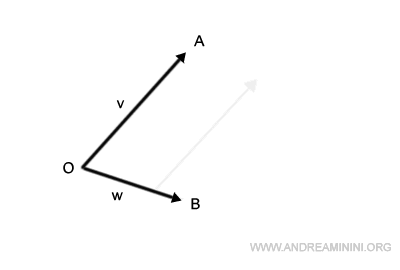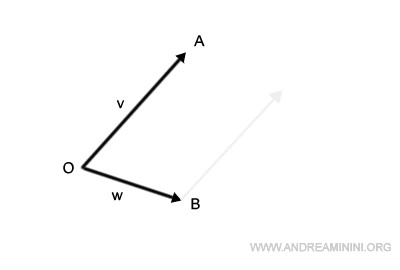
A continuación, trazamos un segmento desde el origen, O, hasta el extremo del vector v desplazado. De este modo obtenemos el vector resultante v+w.

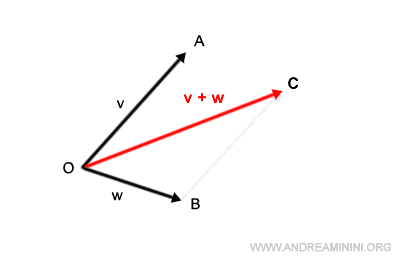
Como se puede observar, este método conduce al mismo resultado que el método del paralelogramo.

Además, el método punta-cola es más directo y permite sumar fácilmente varios vectores de manera sucesiva.

Otro ejemplo:

Veamos ahora cómo sumar tres vectores: v, w y z.

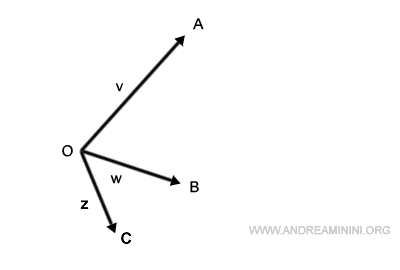
En primer lugar, desplazamos la base del vector w para que coincida con la punta del vector v.

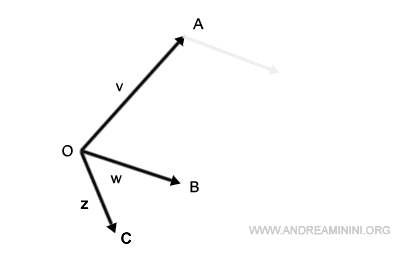
Después colocamos la base del vector z a continuación del nuevo vector w.

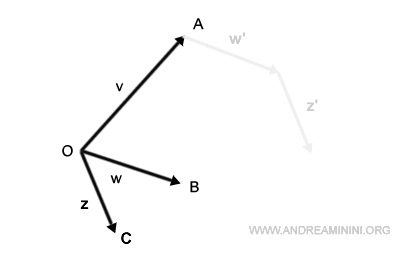
Por último, al trazar un segmento desde el origen hasta el punto final, obtenemos el vector resultante v+w+z.

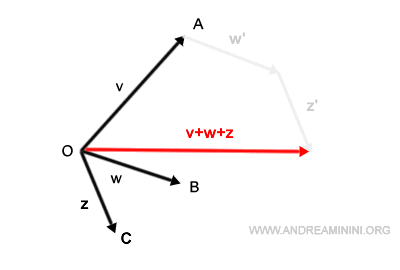
Este método resulta sumamente útil para sumar varios vectores de forma geométrica. Y un aspecto fundamental: el orden en que se sumen los vectores no altera el resultado final. La suma es siempre la misma.

Por ejemplo, aunque alineemos primero el vector v con w y luego añadamos z, el vector resultante v+w+z seguirá siendo el mismo. La gran ventaja de este método es que la suma no depende del orden en que se coloquen los vectores.

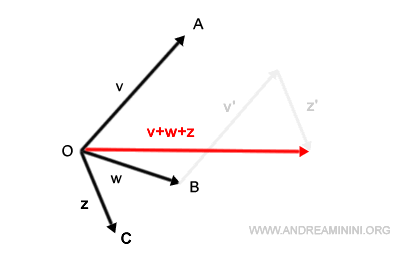
Suma algebraica de vectores

Para determinar el vector resultante, basta con sumar las coordenadas (x, y) de ambos vectores de forma directa: $$ \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} + \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} x_1+x_2 \\ y_1+y_2 \end{pmatrix} $$

Este procedimiento algebraico es especialmente eficaz cuando se trabaja con vectores que tienen más de dos componentes.

Ejemplo

Volvamos a los vectores que hemos utilizado en el ejemplo anterior:

$$ P_1 = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$ $$ P_2 = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \end{pmatrix}$$

Procedemos ahora a calcular la suma algebraica de los vectores OP₁ y OP₂.

Para ello, simplemente sumamos sus respectivas coordenadas x e y:

$$ OP_S = OP_1 + OP_2 = \begin{pmatrix} 1 \\ 2 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \end{pmatrix} $$

El resultado es el vector resultante.

A continuación, representamos este nuevo vector en el plano cartesiano. Observamos que la suma da lugar a un nuevo vector, OP_s.

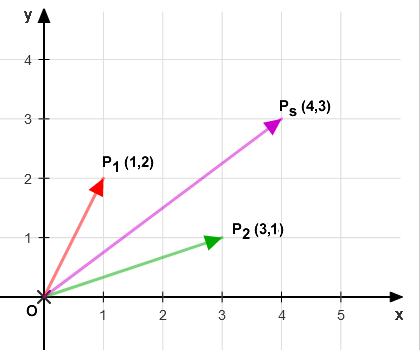
El punto P_s coincide con el vector resultante que ya habíamos obtenido mediante el método del paralelogramo, lo que confirma la consistencia entre ambos enfoques.

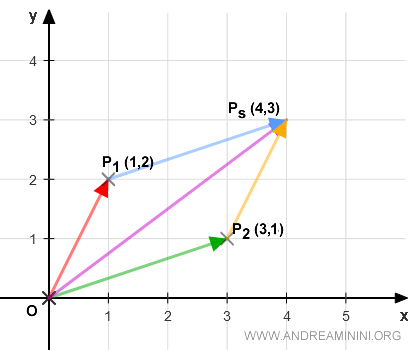
Ejemplo 2

Consideremos ahora dos vectores en un espacio tridimensional (x, y, z):

$$ P_1= \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$ $$ P_2 = \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 4 \end{pmatrix}$$

El vector resultante se obtiene sumando componente a componente:

$$ P_1 + P_2 = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} + \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \begin{pmatrix} x_1 + x_2 \\ y_1 + y_2 \\ z_1 + z_2 \end{pmatrix} = \begin{pmatrix} 1 + 3 \\ 2 + 1 \\ 3 + 4 \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \\ 7 \end{pmatrix} $$

Este procedimiento es totalmente generalizable y se aplica de igual modo a vectores de cualquier dimensión.

Ejemplo 3

Pasemos ahora a un espacio de cuatro dimensiones (x₁, x₂, x₃, x₄):

$$ v = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} $$ $$ w = \begin{pmatrix} 3 \\ 1 \\ 4 \\ -2 \end{pmatrix}$$

Sumamos las componentes correspondientes:

$$ v + w = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \\ 4 \\ -2 \end{pmatrix} = \begin{pmatrix} 1+3 \\ 2+1 \\ 3+4 \\ 4+(-2) \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \\ 7 \\ 2 \end{pmatrix} $$

Este mismo razonamiento permite sumar cualquier número de vectores, en cualquier dimensión.

Ejemplo 4

Consideremos tres vectores en un espacio de cuatro dimensiones:

$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} $$ $$ v_2 = \begin{pmatrix} 3 \\ 1 \\ 4 \\ -2 \end{pmatrix}$$ $$ v_3 = \begin{pmatrix} -1 \\ 1 \\ 1 \\ 3 \end{pmatrix} $$

El vector resultante se calcula sumando todas las componentes:

$$ v_1 + v_2 + v_3 = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \\ 4 \\ -2 \end{pmatrix} + \begin{pmatrix} -1 \\ 1 \\ 1 \\ -2 \end{pmatrix} = \begin{pmatrix} 1+3+(-1) \\ 2+1+1 \\ 3+4+1 \\ 4+(-2)+3 \end{pmatrix} = \begin{pmatrix} 3 \\ 4 \\ 8 \\ 5 \end{pmatrix} $$

Este procedimiento es sistemático y se puede aplicar sin restricciones.

Método del punto medio en la suma de vectores

Cuando se desea sumar dos vectores alineados en la misma dirección, el método del punto medio resulta muy útil. Consiste en determinar el punto medio, M, entre los extremos de ambos vectores y, a partir de ahí, duplicar el segmento OM.

Este enfoque es especialmente valioso cuando los vectores están alineados, aunque sus módulos sean opuestos o distintos.

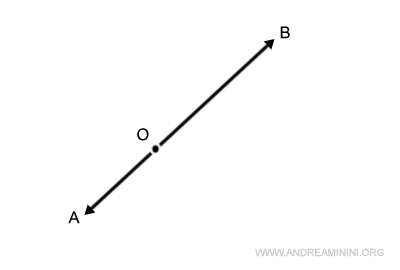
Conviene recordar que si los vectores son opuestos en magnitud, el método del paralelogramo no es aplicable, ya que genera un paralelogramo degenerado. En tales casos, el método del punto medio es el recurso más apropiado. Por otra parte, cuando los vectores son colineales y de igual módulo, la suma se puede obtener de manera inmediata sumando sus magnitudes, sin necesidad de recurrir al punto medio.

Demostración conceptual

En cualquier paralelogramo, las diagonales se cortan en el punto medio de los vértices opuestos.

Dado que el segmento OC representa el módulo del vector suma v+w, basta con trazar la diagonal AB para hallar su punto medio, M.

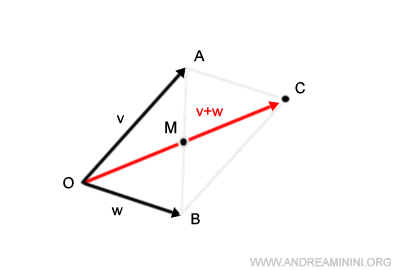
El punto M cumple dos propiedades geométricas clave:

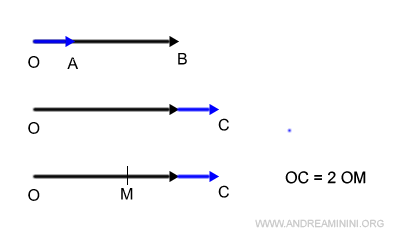
1. Se encuentra a igual distancia de los puntos O y C: $$ OM = MC $$
2. El segmento OM equivale a la mitad del módulo del vector suma (OC): $$ OC = 2 \cdot OM $$

Estas propiedades permiten calcular con precisión la suma de dos vectores que comparten dirección.

Por ejemplo, hallamos el punto medio entre los vértices A y B, obteniendo el segmento OM.

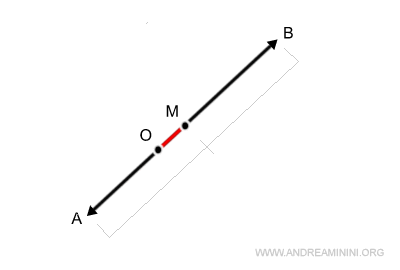
Como OM representa la mitad del módulo del vector suma, basta con duplicarlo para obtener 2 OM, es decir, la magnitud completa del vector suma.

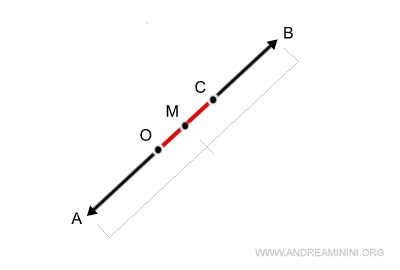
Este es el vector suma:

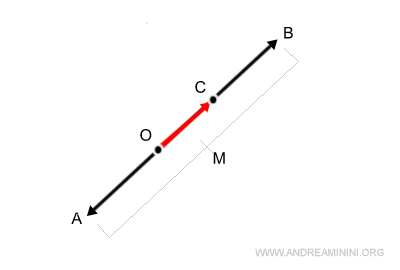
Observación sobre el vector suma. Aunque el método del punto medio puede aplicarse a vectores colineales de igual módulo, en este caso el procedimiento es redundante: basta con sumar directamente sus magnitudes. Determinar el punto medio y duplicarlo no aporta ninguna ventaja adicional en este contexto.

La esencia de la desigualdad triangular

Uno de los principios fundamentales en el álgebra vectorial es la desigualdad triangular. Esta afirma que el módulo (o norma) de la suma de dos vectores nunca supera la suma de los módulos individuales: $$ | \vec{v} + \vec{w} | \le |\vec{v}|+|\vec{w}| $$

 

¿Por qué se denomina "desigualdad triangular"?

El nombre proviene de una propiedad básica de los triángulos: en cualquier triángulo, la suma de las longitudes de dos lados siempre es mayor que la del tercer lado.

Existe un caso particular en el que la desigualdad se convierte en igualdad: cuando los vectores son paralelos y apuntan en la misma dirección. En este caso: $$ | \vec{v} + \vec{w} | = |\vec{v}|+|\vec{w}| $$

El vector resultante conserva entonces la misma dirección y sentido que los vectores originales.

Y así sucesivamente.