Integral de línea
Una integral de línea (también denominada integral curvilínea) es una magnitud escalar que se obtiene al sumar los productos escalares de los vectores v a lo largo de una curva L dentro de un campo vectorial C. $$ \int_A^B \vec{v} \cdot dl $$
Aquí, dl representa un desplazamiento infinitesimal a lo largo de la curva, desde el punto A hasta el punto B.
El vector VP es el vector tangente a la curva en un punto dado P.
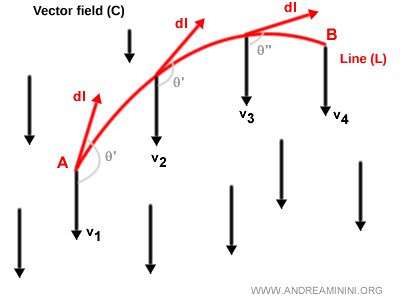
La suma de todos estos productos escalares, V·dl, da como resultado un valor escalar conocido como integral de línea o integral curvilínea.
Aplicaciones En física, las integrales de línea resultan especialmente útiles para calcular el trabajo realizado al desplazar un objeto en un campo de fuerzas.
Un ejemplo práctico
Consideremos un campo vectorial constante C, en el que todos los vectores tienen la misma magnitud, dirección y orientación.
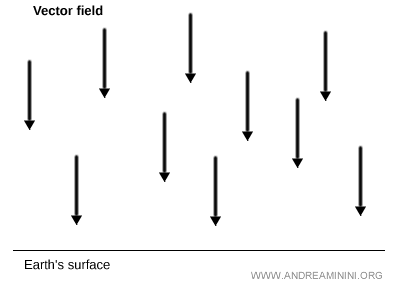
El campo gravitatorio cerca de la superficie terrestre es un ejemplo típico de este tipo de campo vectorial constante.
Los vectores representan la dirección, orientación e intensidad de la fuerza gravitatoria (g).
Para desplazar un objeto en línea recta desde el punto A hasta el punto B con velocidad constante, es necesario realizar un cierto trabajo W para contrarrestar la gravedad.
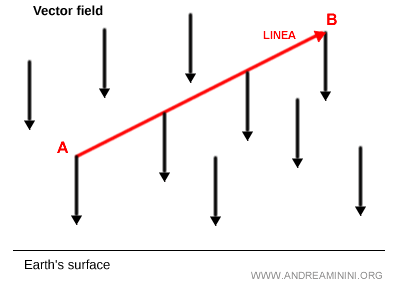
La integral de línea proporciona un método para calcular el valor escalar de la fuerza F implicada.
El recorrido de A a B se divide en segmentos infinitesimales dl.
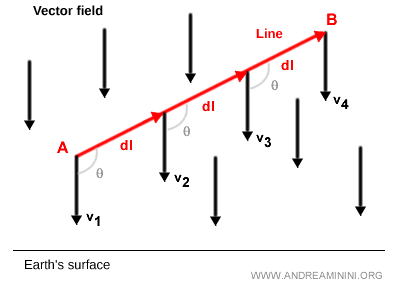
Nota. En este ejemplo, la curva L es una línea recta. Por lo tanto, los vectores tangentes dl están alineados con la dirección de la trayectoria. $$ W = F·dl $$
En cada punto P se calcula el producto escalar entre el vector tangente a la trayectoria y el vector del campo gravitatorio en P.
$$ \vec{v_1} \cdot d_l = |v_1| \cdot |dl| \cdot \cos \ θ $$
$$ \vec{v_2} \cdot d_l = |v_2| \cdot |dl| \cdot \cos \ θ $$
$$ \vec{v_3} \cdot d_l = |v_3| \cdot |dl| \cdot \cos \ θ $$
La suma de estos productos escalares corresponde a la integral de línea, es decir, al trabajo total W necesario para trasladar el objeto a lo largo del recorrido de A a B.
$$ \int_A^B \vec{v} \ dl = \sum_p \vec{v}_p \cdot dl $$
Ejemplo 2
Este mismo principio se aplica incluso cuando el campo vectorial no es constante.
Por ejemplo, la fuerza gravitatoria disminuye al alejarse de la Tierra.
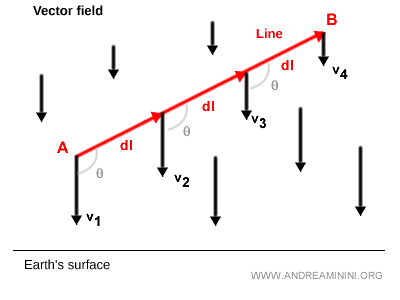
En este caso, los vectores disminuyen en magnitud (longitud) a medida que aumenta la altitud.
Por tanto, el producto escalar varía a lo largo del recorrido.
Ejemplo 3
Cuando la trayectoria no es recta, el recorrido sigue una curva.
En esta situación, es necesario calcular el vector tangente dl en cada punto de la curva.
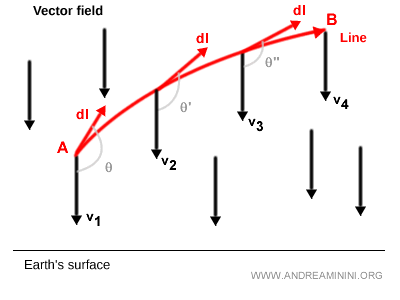
Ahora, los vectores tangentes varían en dirección, magnitud y orientación.
El ángulo θ entre el vector tangente y el vector del campo también varía de forma continua a lo largo de la curva.
Como resultado, el producto escalar cambia de un punto a otro.
Nota. Como alternativa, para aproximar el valor de la integral de línea, se pueden calcular los productos escalares empleando los vectores de una aproximación poligonal de la curva, en lugar de los vectores tangentes exactos en cada punto.
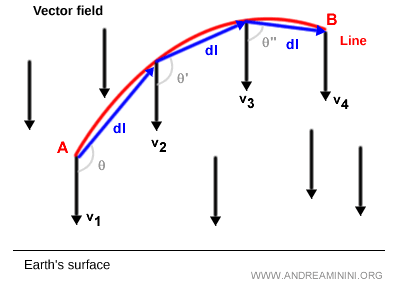
Cada producto escalar representa una cantidad parcial (o elemental) de trabajo. La suma de estos trabajos parciales aproxima el trabajo total necesario para mover el objeto. Cuanto más pequeños sean los segmentos dl en la trayectoria poligonal, menor será el error de aproximación en la integral de línea.
Ejemplo 4
Este mismo enfoque se puede aplicar a campos vectoriales más complejos.
Por ejemplo, al desplazarse por una región con corrientes de aire o de agua variables.
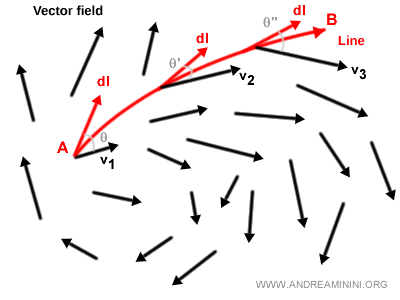
También en este caso, el producto escalar varía continuamente a lo largo de la curva.
Propiedades de las integrales de línea
Las integrales de línea poseen las mismas propiedades que las integrales definidas.
- Si se elige un punto intermedio C dentro del intervalo [A,B], la suma de las integrales de línea sobre los dos subarcos [A,C] y [C,B] es igual a la integral de línea de A a B (propiedad aditiva). $$ \int_A^B \vec{v} \ \cdot dl = \int_A^C \vec{v} \ \cdot dl + \int_C^B \vec{v} \cdot \ dl $$
- Invertir la dirección de recorrido a lo largo de la trayectoria invierte el signo de la integral de línea. $$ \int_A^B \vec{v} \ \cdot dl = - \int_B^A \vec{v} \cdot \ dl $$
Circulación
Circulación se refiere al caso en que los extremos de la curva L coinciden, es decir, A=B y la curva es cerrada. $$ \oint_{L} \vec{v} \cdot dl $$
En este caso, los puntos inicial y final de la curva L son el mismo.
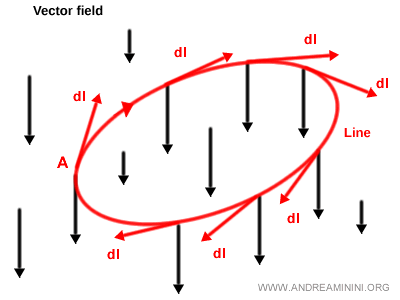
Para indicar la integral de línea en el caso de circulación, se utiliza un símbolo especial, ∮.
$$ \oint_{L} \vec{v} \cdot dl = \int_A^A \vec{v} \cdot dl $$
Invertir la dirección de recorrido a lo largo de la curva cerrada L cambia el signo de la integral de línea.
Y así sucesivamente.