Cálculo Integral
La integral es una herramienta esencial del análisis matemático. Nos permite medir el área que queda bajo la gráfica de una función y el eje x, una idea que está en la base de gran parte de la física, la ingeniería y las matemáticas aplicadas.
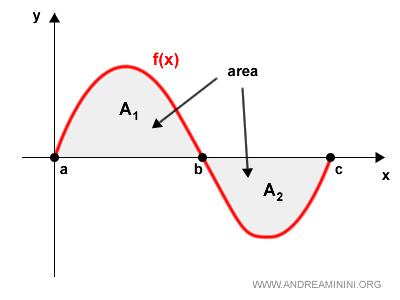
Aunque hoy disponemos de métodos muy avanzados, los primeros pasos hacia el cálculo integral los dieron Arquímedes y Eudoxo de Cnido en el siglo IV a. C., con el método de exhaución. Su objetivo era claro: encontrar el área de figuras que no podían calcularse directamente, acercándose a su valor real mediante aproximaciones sucesivas.
El nombre del método refleja su esencia. La idea es "agotar" el área de la figura mediante polígonos que se ajustan progresivamente a la curva cuya área queremos determinar.
Cómo funciona el método de exhaución
Para ver cómo opera, tomemos como ejemplo el área bajo una parábola en el intervalo [a, b].
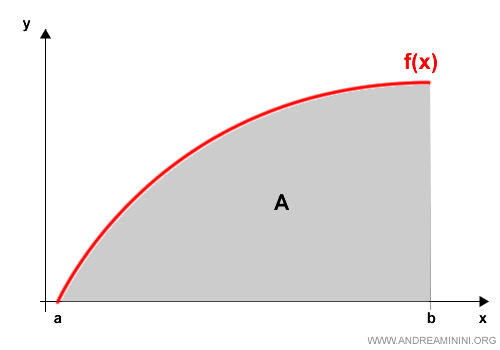
El proceso comienza construyendo varios polígonos inscritos, todos situados dentro de la región delimitada por la curva.
En este ejemplo trabajamos con ocho polígonos: p1, p2, ..., p8.
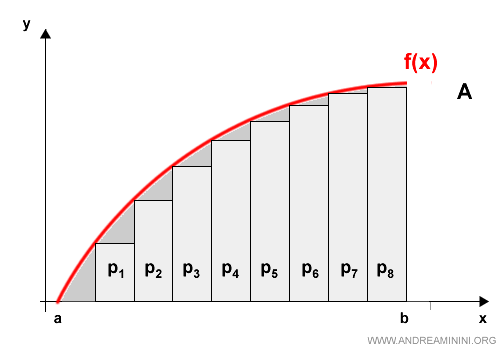
El cálculo del área de cada polígono es directo, y la suma de todas ellas proporciona una cota inferior del área real:
$$ A_{min} = \sum_0^n A(p_n) $$
Para obtener una cota superior, utilizamos polígonos circunscritos, que rodean la parábola desde el exterior.
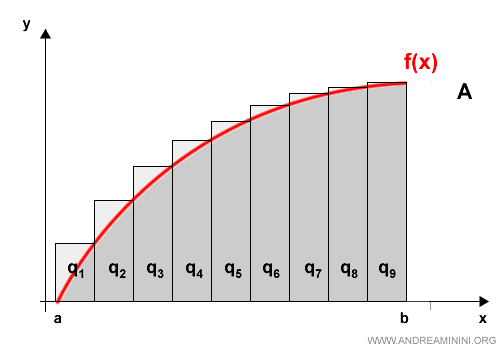
La suma de las áreas de estos polígonos, q1 a q9, ofrece un valor que siempre estará por encima del área buscada:
$$ A_{max} = \sum_0^n A(p_n) $$
Sabemos así que el área real A se encuentra entre las dos aproximaciones:
$$ A_{min} \le A \le A_{max} $$
Nota. Si aumentamos el número de polígonos, ambas estimaciones se acercan cada vez más al valor exacto. En el límite, al usar infinitos polígonos, la cota inferior y la superior coinciden con el área real: $$ \lim_{n \rightarrow \infty} A_{min} = \lim_{n \rightarrow \infty} A_{max} = A $$
Integral definida e integral indefinida
En el estudio del cálculo integral distinguimos dos tipos de integrales, cada una con un propósito concreto:
- Integral definida
Se evalúa en un intervalo específico y da como resultado un número. Es la herramienta que utilizamos cuando queremos calcular áreas bajo curvas. $$ \int_a^b f(x) \:\:dx $$ - Integral indefinida
Representa la antiderivada de la función. No produce un número, sino una expresión general que engloba una familia de funciones. $$ \int f(x) \:\:dx $$
Nota. Aunque estén relacionadas, ambas integrales se utilizan para fines distintos y emplean técnicas diferentes.
El Teorema Fundamental del Cálculo
Si una función es continua en [a, b], entonces la función $$ F(x) = \int_a^x f(t) \: dt $$ es derivable y su derivada coincide con la función original: $$ D[F(x)] = f(x) $$
La función \( F(x) \) se denomina antiderivada o primitiva de \( f(x) \). Este resultado une de forma profunda los dos pilares del cálculo: derivar e integrar.
Un ejemplo para fijar la idea
Consideremos la función \( 2t \) en el intervalo [0, x]. Al integrarla obtenemos:
$$ F(x) = \int_0^x 2t \: dt = x^2 $$
El integrando es:
$$ f(x) = 2x $$
La función integral es:
$$ F(x) = x^2 $$
Y su derivada:
$$ F'(x) = D[x^2] = 2x $$
Por tanto:
$$ F'(x) = f(x) $$
Este ejemplo ilustra perfectamente el Teorema Fundamental del Cálculo.
Por qué funciona: una explicación clara
La clave está en analizar el límite del cociente incremental:
$$ \lim_{h \to 0} \frac{F(x + h) - F(x)}{h} $$
Si aplicamos la propiedad aditiva de las integrales obtenemos:
$$ = \lim_{h \to 0} \frac{1}{h} \left[ \int_x^{x + h} f(t) \: dt \right] $$
Nota: El Teorema del Valor Medio para Integrales garantiza que, en un intervalo tan pequeño, la integral es prácticamente igual al valor de la función en un punto \( x_0 \) multiplicado por la longitud del intervalo. Cuando ese intervalo se hace infinitesimal, \( x_0 \) se acerca a x y el valor tiende a f(x).
Así obtenemos el resultado final:
$$ F'(x) = f(x) $$
Esta demostración cierra el círculo entre derivación e integración, una relación que sostiene gran parte del análisis moderno.
Y a partir de aquí se abren muchos más desarrollos del cálculo integral.