Teorema Fundamental del Cálculo

El Teorema Fundamental del Cálculo establece una idea clave: calcular una integral definida es tan sencillo como evaluar una primitiva en los extremos del intervalo. En concreto: $$ \int_a^b f(x) \:\:dx = F(b) - F(a) $$

¿Qué significa esto?

Una primitiva o antiderivada F(x) es una función cuya derivada es precisamente f(x). Cuando conocemos una primitiva, integrar deja de ser un proceso largo y pasa a ser un cálculo directo.

Nota: No siempre existe una primitiva expresable de forma "bonita", pero cuando sí es posible encontrarla, el cálculo de la integral se simplifica enormemente.

Un ejemplo práctico

Observemos cómo funciona el teorema a través de un ejemplo sencillo:

$$ \int_2^6 3x^2 \:\: dx $$

Una primitiva de 3x² es:

$$ F(x) = x^3 $$

Ya que:

$$ D[x^3] = 3x^2 $$

Entonces aplicamos el teorema directamente:

$$ \int_2^6 3x^2 \:\: dx = 6^3 - 2^3 = 208 $$

Este valor corresponde al área bajo la curva entre x = 2 y x = 6.

Demostración paso a paso

Consideremos dos primitivas distintas F(x) y G(x) de una misma función continua f(t) en el intervalo [a, x].

$$ G(x) = \int_a^x f(t) \: dt \qquad\qquad F(x) = \int_a^x f(t) \: dt $$

Si ambas derivan en f, entonces difieren únicamente en una constante:

$$ G(x) - F(x) = k $$

o, de forma equivalente:

$$ G(x) = F(x) + k $$

Evaluemos ahora en x = a:

$$ G(a) = k + \int_a^a f(t) \: dt = k $$

Por tanto, k = G(a), y podemos escribir:

$$ G(x) = G(a) + \int_a^x f(t) \: dt $$

Si sustituimos x por b:

$$ G(b) = G(a) + \int_a^b f(t) \: dt $$

Reordenando términos se obtiene el resultado esencial:

$$ G(b) - G(a) = \int_a^b f(t) \: dt $$

Este es el corazón del Teorema Fundamental del Cálculo, que conecta derivación e integración en una sola identidad elegante.

Más ejemplos

Ejemplo 1

Tomemos ahora una función constante, uno de los casos más intuitivos:

$$ f(x) = k $$

Su integral definida en cualquier intervalo [a, b] es simplemente el área de un rectángulo:

$$ \int_a^b f(x) \:\: dx = k \cdot (b - a) $$

Por ejemplo, si:

$$ f(x) = 5 $$

entonces:

$$ \int_2^7 5 \:\: dx = 5 \cdot (7 - 2) = 25 $$

Gráficamente se ve así:

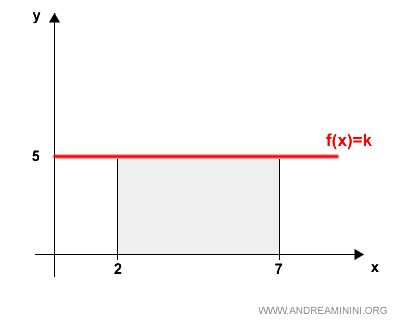
Nota: No importa si el límite superior es menor que el inferior. En ese caso, la integral resulta negativa: $$ \int_7^2 5 \:\: dx = 5 \cdot (2 - 7) = -25 $$ Si ambos límites coinciden, el área es cero: $$ \int_2^2 5 \:\: dx = 5 \cdot (2 - 2) = 0 $$

Estos ejemplos muestran cómo el teorema convierte la integración en una herramienta potente y sorprendentemente directa.