Integral Definida

La integral definida de una función continua f(x) en un intervalo [a,b] se obtiene aplicando la fórmula: $$ \int_a^b f(x) \:\:dx = F(b) - F(a) $$ A este resultado se le conoce como el Teorema Fundamental del Cálculo y establece una relación directa entre integración y derivación.

Los valores a y b se llaman límites de integración, mientras que la función f(x) dentro del símbolo integral es el integrando. La variable x (dx) recibe el nombre de variable de integración.

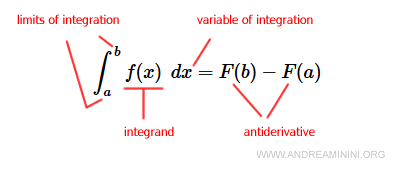
Nota. Una función F(x) es una antiderivada de f(x) cuando su derivada es igual a f(x). $$ D[F(x)+k] = f(x) $$ Por ejemplo, si f(x) = 2x, una antiderivada es F(x) = x² + k, ya que su derivada devuelve exactamente 2x. La constante k no influye al derivar.

¿Qué es la Integral Definida de Riemann?

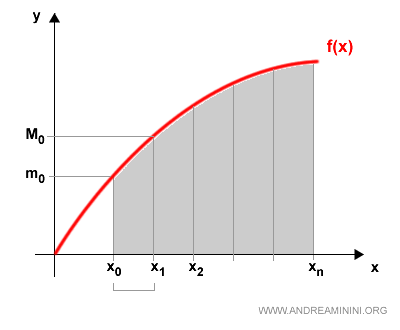
Para entender de manera intuitiva qué significa integrar una función, conviene empezar con una idea sencilla: queremos calcular el área bajo la curva de una función f(x) en un intervalo cerrado [a,b].

Dividimos el intervalo [a,b] en una partición P formada por n+1 puntos:

$$ x_0, x_1, x_2, \ldots, x_n $$

Aquí, x₀ corresponde al extremo izquierdo a y x_n al extremo derecho b.

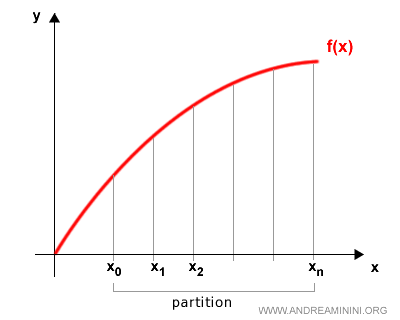
Cada partición genera varios subintervalos:

$$ [x_{k-1}, x_k] \qquad \text{para} \qquad k = 1, \ldots, n $$

En cada uno de estos subintervalos, la función alcanza un mínimo y un máximo:

$$ m_k = \inf \{ f(x) : x \in [x_{k-1}, x_k] \} $$

$$ M_k = \sup \{ f(x) : x \in [x_{k-1}, x_k] \} $$

Por ejemplo, en el subintervalo inicial [x₀, x₁] hablamos de m₀ y M₀.

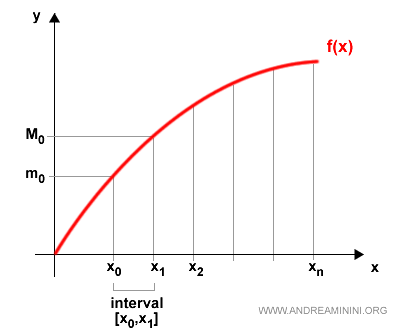
Si tomamos el valor mínimo m_k y lo multiplicamos por la longitud del subintervalo, obtenemos un rectángulo inscrito bajo la curva:

$$ m_k \cdot (x_k - x_{k-1}) $$

Este procedimiento se repite en todos los subintervalos.

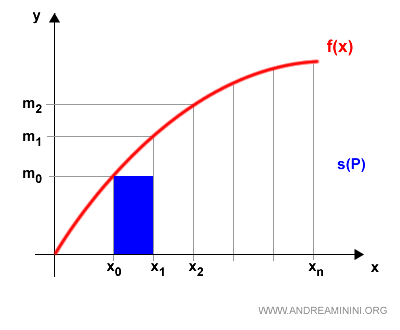
Si en vez del mínimo usamos el máximo M_k, obtenemos los rectángulos circunscritos:

$$ M_k \cdot (x_k - x_{k-1}) $$

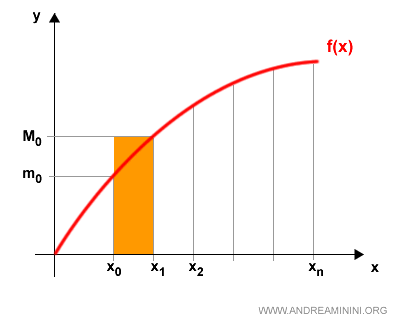
La suma global de todos los rectángulos construidos con los valores mínimos se llama suma inferior de Riemann:

$$ s(P) = \sum_{k=1}^{n} m_k \cdot (x_k - x_{k-1}) $$

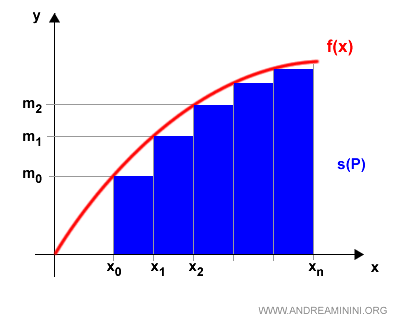
La suma de los rectángulos construidos con los máximos recibe el nombre de suma superior de Riemann:

$$ S(P) = \sum_{k=1}^{n} M_k \cdot (x_k - x_{k-1}) $$

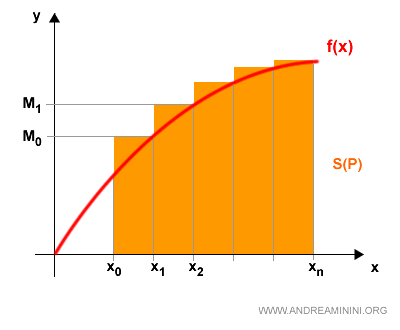
Dado que siempre se cumple m_k ≤ M_k, también se cumple:

$$ s(P) \le S(P) $$

La diferencia entre ambas sumas encierra toda la incertidumbre que tenemos sobre el área real. Lo fundamental es que esta diferencia puede hacerse tan pequeña como queramos afinando la partición.

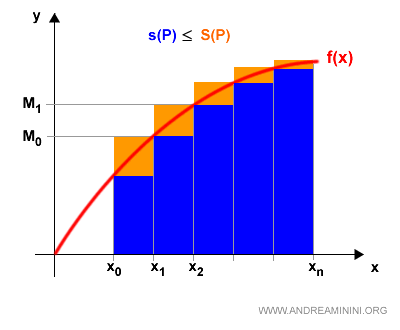
El área verdadera bajo la curva debe encontrarse entre estas dos estimaciones:

Si usamos una partición más fina Q, obtenemos nuevas sumas superior e inferior:

$$ s(Q) \\ S(Q) $$

Cuantos más subintervalos introducimos, menor se vuelve la diferencia entre ambas sumas.

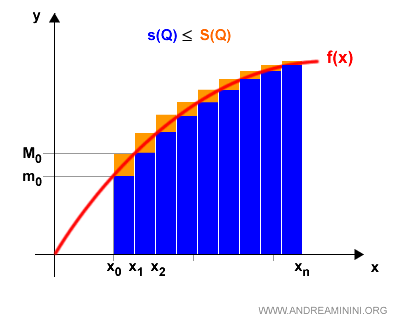
Nota. En la representación gráfica, el área naranja corresponde a la diferencia S(Q) - s(Q). Se aprecia claramente que esta diferencia es mucho menor que la obtenida para la partición P. Afinar la partición mejora la aproximación de forma sistemática.

Definimos ahora los conjuntos que agrupan todas las sumas posibles:

$$ A = \{s(P), s(Q) \} $$

$$ B = \{S(P), S(Q) \} $$

Las sumas inferiores forman el conjunto A y las superiores forman el conjunto B. Estos conjuntos no se superponen.

Si existe un único número c que separa ambos conjuntos, entonces la función f(x) es integrable en el sentido de Riemann. $$ c = \sup A = \inf B $$ Este número c es la integral definida de f(x) en [a,b] y se expresa como: $$ \int_a^b f(x) \:\: dx $$

Un Ejemplo Práctico

Tomemos como punto de partida una función sencilla pero útil para ilustrar el proceso de integración:

$$ f(x) = 3x^2 $$

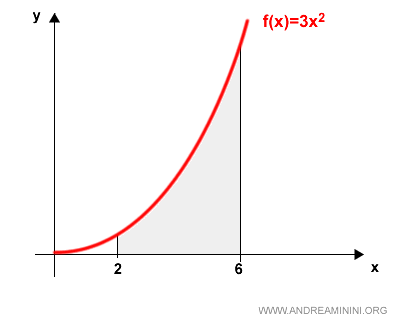
Su gráfica nos permite visualizar de inmediato el comportamiento de la función y el área que deseamos calcular:

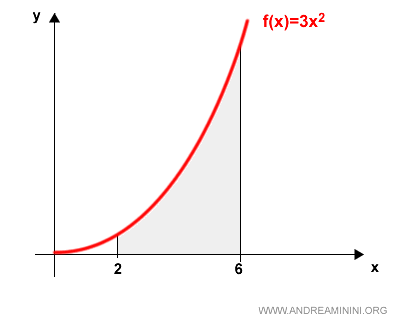
El objetivo es determinar el área bajo la curva en el intervalo [2,6]. Para ello, evaluamos la integral definida:

$$ \int_2^6 3x^2 \: dx $$

Para comprender el método desde cero, comenzamos dividiendo el intervalo en dos partes iguales mediante la partición P.

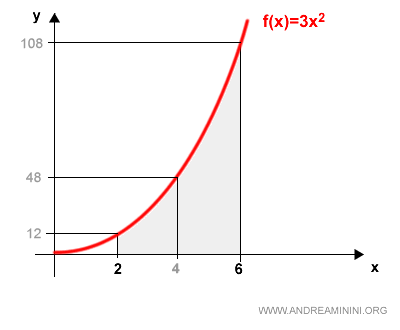
Esta partición nos permite construir dos tipos de aproximaciones geométricas: rectángulos inscritos y rectángulos circunscritos.

Veamos primero los inscritos:

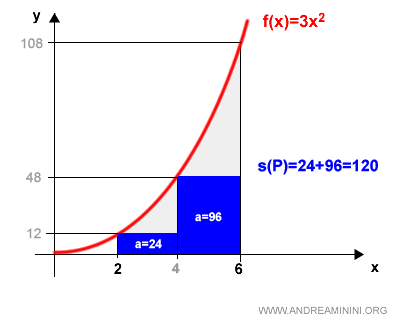
Los rectángulos obtenidos tienen áreas de 24 y 96, por lo que la suma inferior resulta ser:

$$ s(P) = 120 $$

Ahora observamos los rectángulos circunscritos:

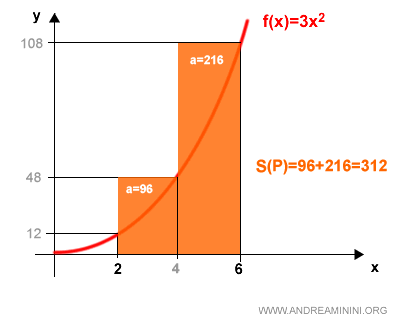
En este caso, las áreas son 96 y 216, dando lugar a la suma superior:

$$ S(P) = 312 $$

El área real se encuentra entre ambas estimaciones:

$$ 120 \leq \text{Área} \leq 312 $$

La comparación gráfica ayuda a visualizar ese margen de incertidumbre:

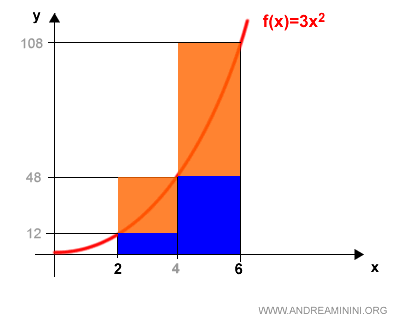
Para mejorar la aproximación, afinamos la partición. La nueva partición Q divide el intervalo en cuatro subintervalos iguales.

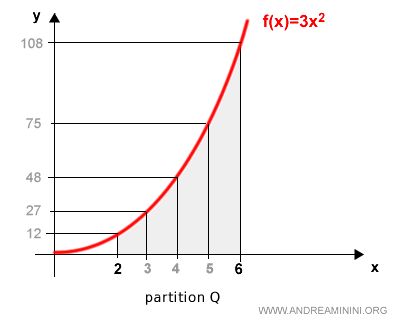
Esto genera nuevas sumas inferior y superior.

Primero, los rectángulos inscritos:

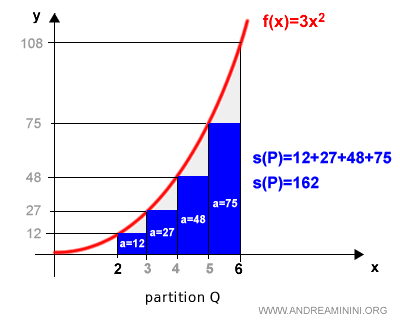
$$ s(Q) = 162 $$

Ahora los rectángulos circunscritos:

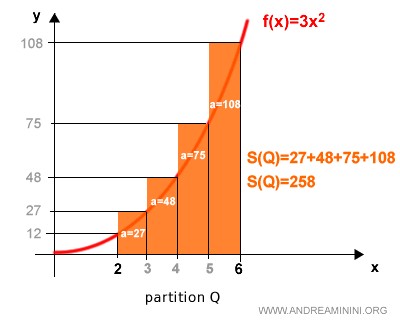
$$ S(Q) = 258 $$

Recopilando los resultados:

$$ s(P) = 120, \quad S(P) = 312 $$

$$ s(Q) = 162, \quad S(Q) = 258 $$

Las sumas inferiores forman el conjunto A:

$$ A = \{120, 162\} $$

Las sumas superiores forman el conjunto B:

$$ B = \{312, 258\} $$

Sus cotas respectivas son:

$$ \sup(A) = 162, \qquad \inf(B) = 258 $$

La definición de Riemann establece que el área exacta debe encontrarse entre estas dos cotas:

$$ 162 \leq \text{Área} \leq 258 $$

A medida que dividimos el intervalo en segmentos más pequeños, la diferencia entre la suma inferior y la suma superior se va estrechando. En el límite, ambas convergen al valor exacto de la integral definida.

Cuando finalmente coinciden, hemos determinado el área real bajo la curva.

El Teorema Fundamental del Cálculo

Las sumas de Riemann son esenciales para construir el concepto de integral, pero no son el método más práctico para calcularla. Existe una vía mucho más directa.

El Teorema Fundamental del Cálculo establece que si conocemos una antiderivada de f(x), entonces podemos evaluar la integral definida exactamente.

$$ \int_a^b f(x) \:\:dx = F(b) - F(a) $$

Esto transforma el cálculo de un área en una simple evaluación de una función en dos puntos.

Nota. El teorema exige que la función sea continua en el intervalo. En algunos casos, encontrar una antiderivada explícita puede ser complicado, pero cuando es posible, el proceso se simplifica enormemente.

Ejemplo

Apliquemos el teorema a nuestra función:

$$ \int_2^6 3x^2 \:\: dx $$

Una antiderivada es:

$$ F(x) = x^3 $$

Ya que su derivada es:

$$ D[x^3] = 3x^2 $$

Evaluando la antiderivada en los límites obtenemos:

$$ \int_2^6 3x^2 \:\: dx = 6^3 - 2^3 = 208 $$

Este es el valor exacto del área bajo la curva entre x = 2 y x = 6.

Este ejemplo muestra cómo el Teorema Fundamental del Cálculo convierte un proceso aproximado en un cálculo preciso y directo.