Integración por Sustitución

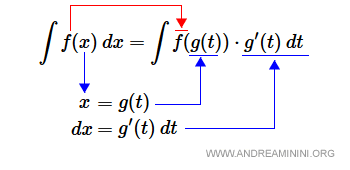
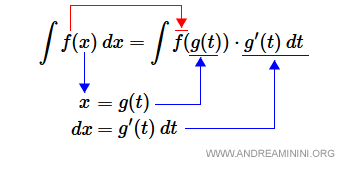
Sea f(x) una función continua y g(x) una función diferenciable con derivada continua. Entonces se cumple: $$ \int f(x) \: dx = \int f(g(t)) \cdot g'(t) \: dt $$ donde \( x = g(t) \).

¿Para qué sirve?

La integración por sustitución es una técnica esencial en el cálculo de integrales indefinidas. Permite transformar un integrando complicado en otro más manejable, aprovechando la relación entre composición de funciones y derivación.

Dos formas de aplicar la sustitución

La fórmula puede aplicarse en sentido directo o inverso, según convenga para simplificar el integrando.

• Primer enfoque: Se sustituye la variable \( x \) por \( g(t) \) y se reemplaza \( dx \) por \( g'(t)\,dt \). La función f se mantiene, solo cambia la variable de integración.
  
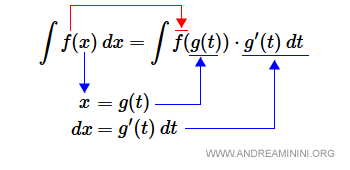
• Segundo enfoque: Cuando el integrando tiene la estructura típica \( f(g(x)) \cdot g'(x) \), la sustitución permite identificar directamente la variable interna. Basta asignar \( t = g(x) \) y usar \( dt = g'(x)\,dx \).
  

¿Qué método elegir? La elección depende por completo del integrando. A veces conviene transformar primero la variable, en otras es más práctico identificar rápidamente la función interna. La intuición mejora con la práctica.

Ejemplos Resueltos

Ejemplo 1

Calcular:

$$ \int \frac{ \sin \sqrt{x} }{\sqrt{x}} \: dx $$

Aplicamos el primer método de sustitución.

La presencia de \( \sqrt{x} \) dificulta la integral, por lo que definimos:

$$ t = \sqrt{x} $$

$$ x = t^2 $$

$$ dx = \frac{d}{dt}(t^2)\,dt = 2t \, dt $$

Sustituimos en la integral:

$$ \int \frac{\sin \sqrt{x}}{\sqrt{x}}\,dx = \int \frac{\sin t}{t} \cdot 2t \, dt $$

$$ = \int 2 \sin t \, dt $$

$$ = 2 \int \sin t \, dt $$

$$ = -2 \cos t + c $$

Volvemos a la variable original:

$$ = -2 \cos(\sqrt{x}) + c $$

Ejemplo 2

Calcular:

$$ \int \cos x \cdot \sin ( \sin x ) \: dx $$

Aquí el integrando es claramente una función compuesta, pues \( \cos x \) es la derivada de \( \sin x \). Este es un caso ideal para el segundo método de sustitución.

Definimos:

$$ t = \sin x $$

$$ dt = \cos x \, dx $$

Sustituimos:

$$ \int \cos x \cdot \sin(\sin x)\,dx = \int \sin(t) \, dt $$

Integral inmediata:

$$ = -\cos t + c $$

Volvemos a x:

$$ = -\cos(\sin x) + c $$

Ejemplo 3

Evaluar:

$$ \int \frac{1}{\sqrt{x} - 3} \: dx $$

Usamos nuevamente el primer método de sustitución.

Sea:

$$ x = t^2 $$

$$ dx = 2t\,dt $$

Sustituimos en la integral:

$$ \int \frac{1}{\sqrt{x} - 3}\,dx = \int \frac{1}{t - 3} \cdot 2t \, dt $$

$$ = 2 \int \frac{t}{t - 3} \, dt $$

Reescribimos el numerador:

$$ = 2 \int \frac{(t - 3) + 3}{t - 3} \, dt $$

Separación de términos:

$$ = 2 \left[ \int 1 \, dt + 3 \int \frac{1}{t - 3} \, dt \right] $$

Integramos:

$$ = 2 \left[ t + 3 \log |t - 3| \right] + c $$

Volvemos a x:

$$ = 2 \sqrt{x} + 6 \log| \sqrt{x} - 3 | + c $$

Por tanto:

$$ \int \frac{1}{\sqrt{x} - 3} \: dx = 2 \sqrt{x} + 6 \log| \sqrt{x} - 3 | + c $$

Fundamento Teórico

La integración por sustitución se apoya en la regla de la cadena, uno de los pilares del cálculo diferencial.

$$ \frac{d}{dt}F(g(t)) = F'(g(t)) \cdot g'(t) $$

Al integrar ambos miembros:

$$ \int \frac{d}{dt}F(g(t)) \: dt = \int F'(g(t)) \cdot g'(t) \: dt $$

Como la integración revierte la diferenciación:

$$ F(g(t)) = \int F'(g(t)) \cdot g'(t) \: dt $$

Si \( F'(g(t)) = f(g(t)) \), entonces:

$$ F(g(t)) = \int f(g(t)) \cdot g'(t) \: dt $$

Es decir:

$$ \int f(g(t)) \: dt = \int f(g(t)) \cdot g'(t) \: dt $$

Usando la relación \( x = g(t) \), se obtiene:

$$ \int f(x) \: dx = \int f(g(t)) \cdot g'(t) \: dt $$

Este resultado resume la justificación formal del método de sustitución.