Integrales triples

Una integral triple amplía la idea de la integral doble a funciones de tres variables, \( f(x, y, z) \), definidas sobre una región sólida \( E \subseteq \mathbb{R}^3 \). Se representa mediante la expresión: \[\iiint_E f(x, y, z)\, dV\] donde \( dV \) es un elemento de volumen infinitesimal, como \( dx\,dy\,dz \), y \( E \) es una región tridimensional del espacio.

A primera vista, la interpretación geométrica y física de una integral triple puede resultar poco intuitiva, ya que involucra volúmenes en lugar de áreas.

De forma intuitiva, si \( f(x, y, z) \geq 0 \), la integral triple calcula la cantidad total de una magnitud distribuida en el espacio, como masa, energía o carga eléctrica, de acuerdo con la función de densidad \( f \):

$$ \iiint_E f(x, y, z)\, dV $$

Cuando la función \( f(x, y, z) \) toma valores positivos y negativos, la integral mide la contribución neta, es decir, el balance entre lo que la función añade al volumen y lo que resta:

$$ \iiint_E f(x, y, z)\, dV = \text{parte positiva} - \text{parte negativa} $$

Por ejemplo, si \( f(x, y, z) \) describe una densidad, las regiones donde \( f > 0 \) aportan material, es decir masa positiva, mientras que las regiones donde \( f < 0 \) representan una sustracción, un déficit o masa negativa. La integral resume el balance global entre lo que está presente y lo que falta. En contextos de física o ingeniería, una función que cambia de signo puede modelar flujos opuestos, como entrada y salida.

¿Cómo se calcula una integral triple?

En la práctica, una integral triple se evalúa como una integral iterada, eligiendo un orden de integración que se adapte a la geometría de la región considerada:

\[ \iiint_E f(x, y, z)\, dV = \int_{x_0}^{x_1} \int_{y_0(x)}^{y_1(x)} \int_{z_0(x,y)}^{z_1(x,y)} f(x, y, z)\, dz\,dy\,dx \]

El orden de integración puede cambiarse, por ejemplo \( dz\,dx\,dy \), según la forma del dominio \( E \).

Es importante tener en cuenta que, aunque el valor de la integral no depende del orden elegido, los límites de integración deben redefinirse cuidadosamente para describir correctamente la región en cada caso.

Un ejemplo práctico

Calculemos la integral triple de la función \[ f(x, y, z) = z \] sobre el cubo \[ E = [0,1] \times [0,1] \times [0,1] \]

En este ejemplo, la función \( f(x, y, z) = z \) representa una densidad que aumenta linealmente con la altura.

La integral nos da la cantidad total contenida en el cubo, por ejemplo la masa total, suponiendo que la densidad depende de \( z \).

Escribimos la integral en forma iterada:

\[ \iiint_E z\, dV = \int_0^1 \int_0^1 \int_0^1 z\, dz\,dy\,dx \]

Comenzamos integrando con respecto a \( z \):

\[ \int_0^1 z\, dz = \left[ \frac{z^2}{2} \right]_0^1 = \frac{1}{2} \]

A continuación, integramos con respecto a \( y \):

\[ \int_0^1 \frac{1}{2}\, dy = \frac{1}{2} \]

Y finalmente, con respecto a \( x \):

\[ \int_0^1 \frac{1}{2}\, dx = \frac{1}{2} \]

El valor final de la integral triple es:

\[ \iiint_E z\, dV = \frac{1}{2} \]

Esto significa que la masa total en el cubo es \( \frac{1}{2} \) unidades. Como la densidad aumenta desde cero en la base (\( z = 0 \)) hasta uno en la parte superior (\( z = 1 \)), el resultado coincide con el valor medio de \( z \) multiplicado por el volumen del cubo.

El valor medio de \( z \) en el cubo unidad es \( \frac{1}{2} \) y, dado que el volumen es \( 1 \), la integral devuelve \( \frac{1}{2} \times 1 = \frac{1}{2} \).

Ejemplo 2

Consideremos ahora la función \( f(x, y, z) = z - 0.5 \), nuevamente sobre el cubo unidad \( E = [0,1]^3 \). Esta función es negativa por debajo del plano \( z = 0.5 \) y positiva por encima de él.

La integral triple se escribe como:

\[ \iiint_E (z - 0.5)\, dV = \int_0^1 \int_0^1 \int_0^1 (z - 0.5)\, dz\,dy\,dx \]

Empezamos evaluando la integral más interna:

\[ \int_0^1 (z - 0.5)\, dz = \left[ \frac{z^2}{2} - 0.5z \right]_0^1 = \left( \frac{1}{2} - 0.5 \right) = 0 \]

Dado que este resultado es cero, las dos integrales restantes también se anulan:

\[ \int_0^1 \int_0^1 0\, dy\,dx = 0 \]

Por lo tanto, el valor de la integral triple es:

\[ \iiint_E (z - 0.5)\, dV = 0 \]

Este resultado refleja la simetría de la función \( z - 0.5 \), que aporta valores negativos por debajo de \( z = 0.5 \) y valores positivos de igual magnitud por encima. Ambas contribuciones se compensan exactamente.

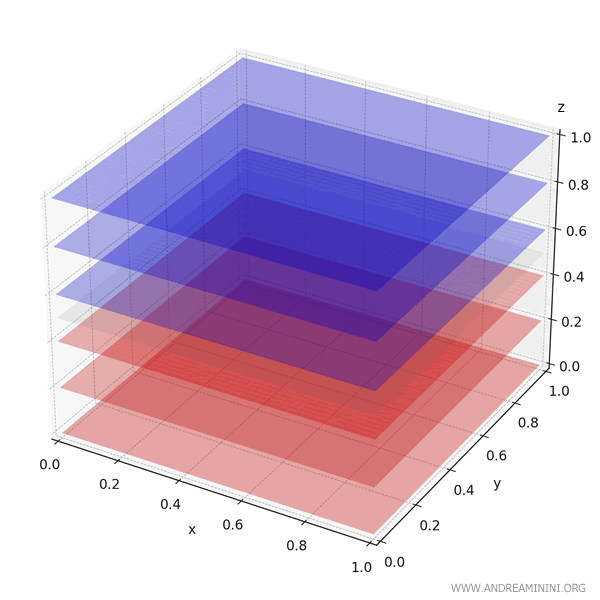
Este gráfico tridimensional de \( f(x, y, z) = z - 0.5 \) sobre el cubo \( [0,1]^3 \) muestra claramente:

• Capas azules, donde la función es positiva, por encima de \( z = 0.5 \)
• Capas rojas, donde la función es negativa, por debajo de \( z = 0.5 \)

Debido a la simetría respecto al plano \( z = 0.5 \), las contribuciones positivas y negativas se cancelan entre sí, dando como resultado una integral neta nula.

Nota. Desde un punto de vista físico, este caso puede interpretarse como la acción de fuerzas iguales y opuestas, por ejemplo un empuje y una tracción, que se equilibran mutuamente.

Y así sucesivamente.