Primitivas (Antiderivadas)
¿Qué es una primitiva?
Una primitiva es una función F(x) cuya derivada reproduce exactamente a otra función f(x). Es decir, F(x) es diferenciable en un intervalo [a, b] y cumple: $$ F'(x) = f(x) \quad \text{para todo } x \in [a, b] $$
Este concepto es fundamental en cálculo, porque establece el puente entre derivación e integración.
Un ejemplo sencillo para comenzar
Tomemos la función:
$$ F(x) = x^2 $$
Si la derivamos, obtenemos:
$$ F'(x) = 2x $$
Esto quiere decir que F(x) = x² es una primitiva de f(x) = 2x. Es una idea simple pero poderosa, porque está en el corazón del Teorema Fundamental del Cálculo.
Cómo reconocer una primitiva
Si f(x) es continua en [a, b], una función F(x) es una primitiva de f(x) siempre que su derivada sea f(x): $$ F(x) = \int_a^b f(x) \: dx $$
Además, toda función continua f(x) tiene infinitas primitivas. Todas se diferencian solo en una constante:
$$ F(x) + k $$
Esto ocurre porque la derivada de una constante siempre es cero.
Ejemplo: Consideremos las funciones F(x) = x² + 3 y G(x) = x² + 5. Ambas tienen la misma derivada:
$$ F'(x) = 2x \\ G'(x) = 2x $$Por eso, cuando integramos 2x, escribimos:
$$ \int 2x \: dx = x^2 + k $$La constante k representa todas las primitivas posibles.
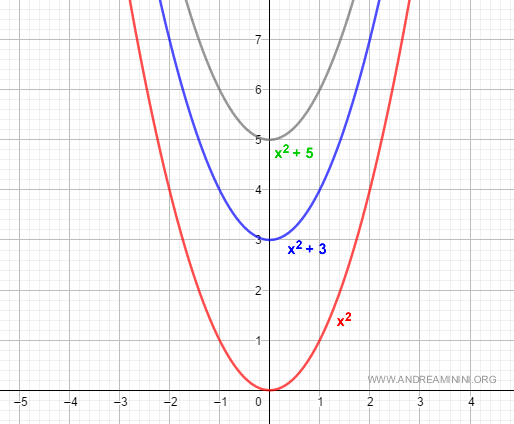
Por qué todas las primitivas se diferencian en una constante
Si F(x) y G(x) son primitivas de la misma función, su diferencia es constante. Para verlo definimos:
$$ H(x) = G(x) - F(x) $$
Al derivar H(x) obtenemos:
$$ H'(x) = G'(x) - F'(x) = f(x) - f(x) = 0 $$
Una función con derivada cero es constante, por lo que:
$$ G(x) = F(x) + k $$
Las primitivas son funciones continuas
Si f(x) es continua en un intervalo, cualquier primitiva F(x) también lo será.
Este hecho se desprende directamente del Teorema Fundamental del Cálculo: la derivada de F(x) existe y es igual a f(x), de modo que F(x) debe ser continua.
Ejemplo
Sea:
$$ f(x) = x^2 $$
que es continua en \((-1, 1)\). Una primitiva es:
$$ F(x) = \frac{x^3}{3} + C $$
Esta función también es continua en el mismo intervalo.
Nota: Cuando f(x) no es continua, la situación puede cambiar bastante. Dos casos ilustrativos:
- Caso 1: $$ f(x) = \frac{1}{x} $$ Es discontinua en \( x = 0 \). Su primitiva \( F(x) = \ln |x| + C \) tampoco está definida en ese punto. Aquí, la falta de continuidad se transmite a la primitiva.
- Caso 2: $$ f(x) = \frac{1}{\sqrt{|x|}} $$ No está definida en \( x = 0 \). Sin embargo, su primitiva \( F(x) = 2\sqrt{|x|} \) sí es continua en \( x = 0 \). Este caso muestra que no siempre existe una relación directa entre la continuidad de f(x) y la de sus primitivas.
Estos ejemplos ayudan a entender que las primitivas dependen profundamente del comportamiento de la función original.
Este conjunto de ideas constituye la base de la integración indefinida y de gran parte del análisis en una variable.