Derivada de una función
¿Qué es una derivada?
La derivada de una función $f(x)$ en un punto $x$ se define como el límite del cociente incremental:
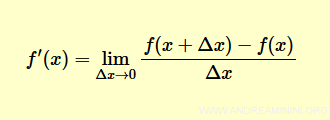
Este límite se denomina primera derivada y se representa con $f'(x)$.
El procedimiento mediante el cual se calcula este límite recibe el nombre de diferenciación.
Ejemplo
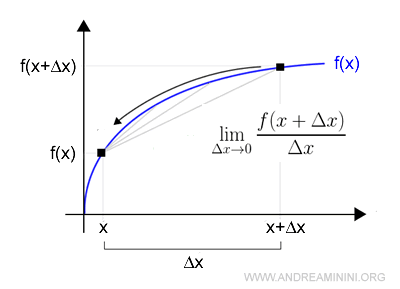
La primera derivada puede expresarse con distintas notaciones equivalentes:
$$ f'(x)=Df=\frac{dy}{dx}=y' $$
La forma $\tfrac{dy}{dx}$ es la llamada notación de Leibniz.
Nota. La primera derivada $f'(x)$ es a su vez una función, que puede derivarse nuevamente. La derivada de la derivada recibe el nombre de segunda derivada, y se denota $f''(x)$, y así sucesivamente.
Condiciones de derivabilidad
Una función $f(x)$ definida en un intervalo $(a, b)$ se dice derivable en un punto $x$ si existe el límite del cociente incremental cuando $h$ tiende a cero.
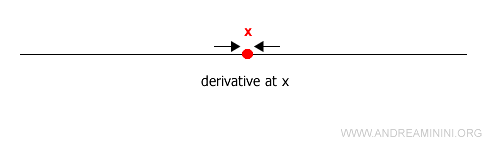
Decimos que una función es derivable en un intervalo abierto $(a, b)$ si lo es en cada punto $x$ estrictamente comprendido entre $a$ y $b$:
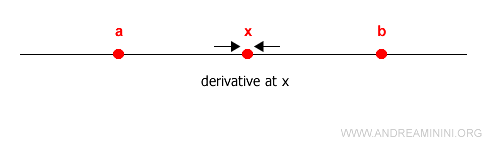
Asimismo, una función es derivable en un intervalo cerrado $[a,b]$ si es derivable en todos sus puntos interiores y, además, existe la derivada lateral derecha en $x = a$ y la derivada lateral izquierda en $x = b$.
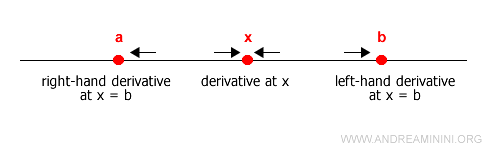
Los puntos en los que la derivada no existe se denominan puntos singulares.
Derivadas laterales
En algunos casos, una función no es derivable en un punto $x$, pero sí admite derivada por la izquierda y por la derecha de dicho punto.
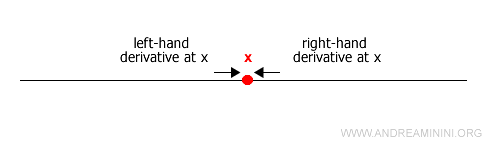
En tales situaciones, los límites finitos calculados al aproximarse por la izquierda y por la derecha reciben el nombre de derivada lateral izquierda y derivada lateral derecha en $x$, respectivamente.
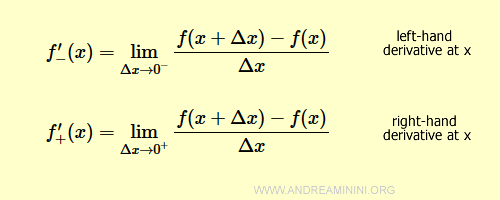
¿Cuál es la diferencia?
En la derivada lateral izquierda, el incremento $\Delta x$ tiende a 0 por valores negativos ($\Delta x < 0$).
En la derivada lateral derecha, $\Delta x$ tiende a 0 por valores positivos ($\Delta x > 0$).
Si una función es derivable en $x$, entonces existen ambas derivadas laterales y coinciden con la derivada ordinaria: $$ f'(x) = f'_-(x) = f'_+(x) $$
Ejemplo práctico
Consideremos la función:
$$ \frac{1}{x} $$
Esta función no está definida en $x = 0$ y, en consecuencia, no es derivable en dicho punto.
Por ello, $x = 0$ constituye un punto singular de $f(x)$.
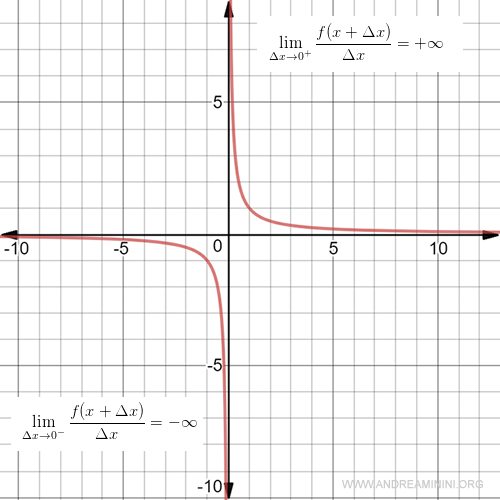
No obstante, en $x = 0$ sí existen derivadas laterales.
La derivada lateral izquierda tiende a menos infinito:
$$ f'_-(x) = \lim_{Δx \rightarrow 0^-} \frac{f(x+Δx)-f(x)}{Δx} = - \infty $$
La derivada lateral derecha tiende a más infinito:
$$ f'_+(x) = \lim_{Δx \rightarrow 0^+} \frac{f(x+Δx)-f(x)}{Δx} = + \infty $$
El análisis de los límites laterales nos permite describir el comportamiento de una función incluso en los puntos donde no está definida.
Corolarios de la derivada
- Si una función es derivable en $x$ y su derivada $f'(x)$ es finita, entonces existen las dos derivadas laterales y ambas coinciden con ella:
$$ \text{Si} \:\: f'(x) = l \;\Rightarrow\; f'(x) = f'_-(x) = f'_+(x) $$
En cambio, si la función no es derivable en $x$, las derivadas laterales pueden no coincidir o incluso no existir.
Notación de Leibniz
Una de las formas más utilizadas para expresar la derivada en cálculo es la notación de Leibniz:
$$ \frac{dy}{dx} $$ o $$ \frac{δy}{δx} $$
El numerador representa la variable dependiente (el valor de la función).
El denominador indica la variable independiente respecto de la cual se efectúa la derivación.
Nota. La notación de Leibniz resulta especialmente útil en el cálculo con varias variables, ya que permite especificar claramente con respecto a qué variable se deriva. En funciones de una sola variable, suele preferirse la notación más concisa $y''$.
Y así sucesivamente.