Derivada y pendiente de la recta tangente

La interpretación geométrica de la derivada de una función f(x) está estrechamente relacionada con la pendiente de la recta tangente en un punto de la curva. $$ f'(x_0) = \tan \:\: \alpha $$ donde α representa la inclinación de la tangente en el punto f(x₀).

Demostración y explicación

Consideremos dos puntos, A y B, en la gráfica de la función:

$$ f(x) $$

$$ f(x+h) $$

donde h es el incremento de la variable independiente x.

La distancia vertical entre ambos puntos viene dada por:

$$ f(x+h) - f(x) $$

Situemos ahora el punto C en la intersección de las rectas paralelas a los ejes coordenados que pasan por A y B.

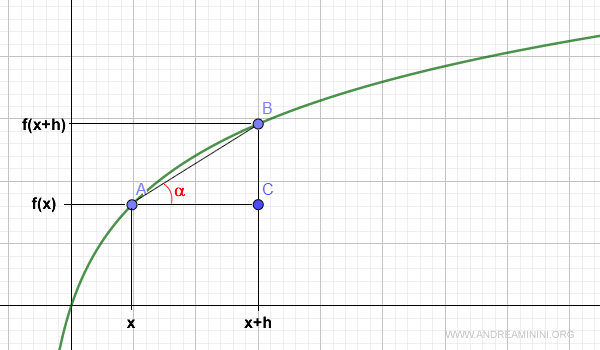
Al unir A, B y C se forma un triángulo rectángulo cuyos lados son:

• AC = h, que corresponde a Δx
• BC = f(x+h) - f(x), que corresponde a Δy

El cociente incremental de la función entre A y B es:

$$ \frac{f(x+h)-f(x)}{h} $$

Este cociente representa la pendiente de la hipotenusa del triángulo, equivalente a &tan; α.

$$ \tan \:\: \alpha = \frac{f(x+h)-f(x)}{h} $$

¿Por qué coincide con la tangente? Si suponemos AB = 1 (radio unitario), la razón BC/AC en el triángulo rectángulo corresponde a la relación seno/coseno en trigonometría.

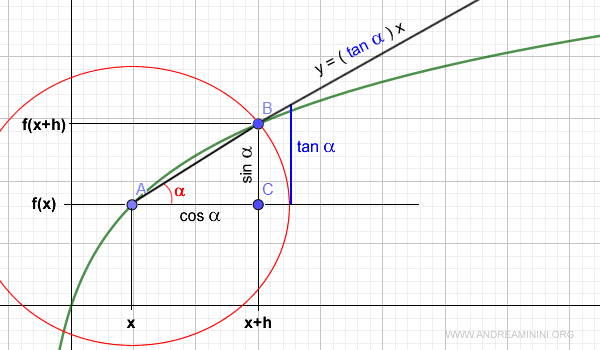
Como la razón seno/coseno es precisamente la tangente, resulta: $$ \frac{BC}{AC} = \frac{\sin \:\alpha}{\cos \:\alpha} = \tan \:\alpha $$

De este modo, el cociente incremental (o tan α) expresa también la pendiente del segmento AB.

Ejemplo. Supongamos que AC = 6 y BC = 4. Entonces, el cociente incremental es BC/AC = 4/6 = 2/3. Así, la tangente del ángulo α es 2/3.

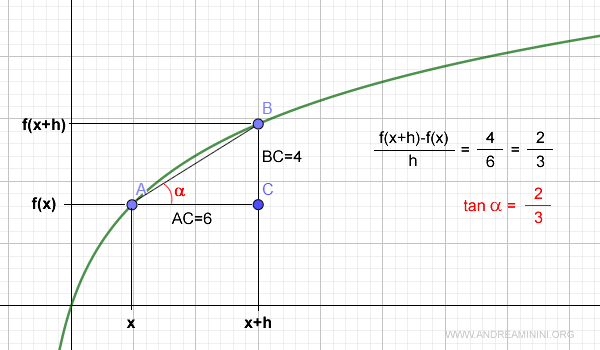
Tan α es también la pendiente de la recta que pasa por A y B. Por tanto, el segmento AB es paralelo a una recta de la forma y = (tan α)x que pasa por el origen; en este caso, y = (2/3)x.

Si la función es derivable en un punto x, podemos calcular el límite del cociente incremental cuando h tiende a cero.

Este límite nos da la derivada de f(x) en el punto x:

$$ \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} = f'(x) $$

El límite del cociente incremental -la derivada- tiene un significado geométrico esencial.

Es igual a la pendiente β de la recta tangente a la curva en el punto x.

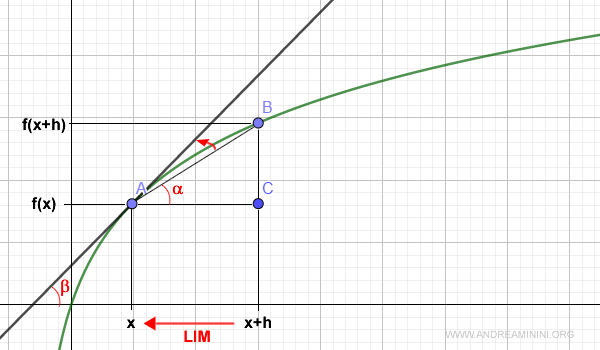
En consecuencia, la ecuación cartesiana de la tangente se escribe:

$$ y = \beta \cdot x $$

Más generalmente, se cumple:

Dado un punto (x₀, y₀) de la función, la ecuación de la recta tangente en x₀ es: $$ y - y_0 = f'(x_0) \cdot (x - x_0) $$

Esta fórmula permite hallar la ecuación de la tangente en (x₀, y₀), salvo en el caso especial de una tangente vertical.

Para verificar si existe una tangente vertical en un punto, debe aplicarse un criterio distinto.

Nota. En un punto x₀ donde la función sea continua, existe tangente vertical si el límite de la derivada en x₀ existe y es +∞ o -∞.

Un ejemplo sencillo

Tomemos como ejemplo la función cuadrática:

$$ f(x) = x^2 $$

Consideremos el punto x = 1 con un incremento h = 1:

$$ f(1) = 1 $$

$$ f(2) = 4 $$

Esto nos da dos puntos, A y B:

$$ A \begin{pmatrix} 1 \\ 1 \end{pmatrix}$$

$$ B \begin{pmatrix} 2 \\ 4 \end{pmatrix}$$

Situamos el punto C:

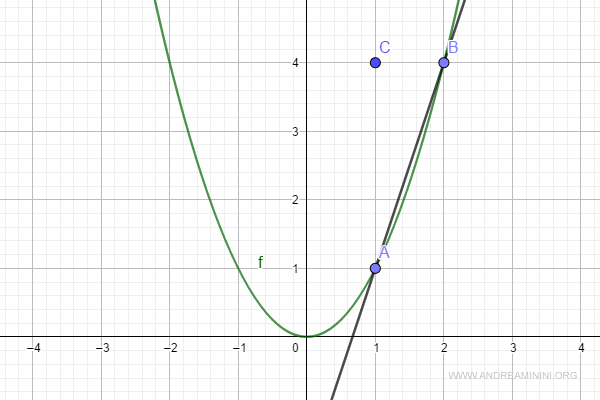
El cociente incremental resulta:

$$ \frac{f(x+h)-f(x)}{h} = \frac{4-1}{1} = 3 $$

Por tanto, el cociente incremental vale 3.

Esto significa que la tangente del ángulo α es 3:

$$ \tan \: \alpha = 3 $$

En consecuencia, la pendiente (m) del segmento AB es 3.

Para determinar la ecuación cartesiana de la recta que pasa por A y B, usamos la forma punto-pendiente:

$$ y - y_0 = m \cdot (x - x_0) $$

Con m = 3:

$$ y - y_0 = 3 \cdot (x - x_0) $$

Tomando como referencia el punto A (1, 1):

$$ y - 1 = 3 \cdot (x - 1) $$

$$ y = 3x - 2 $$

Así obtenemos la ecuación de la recta que pasa por A y B.

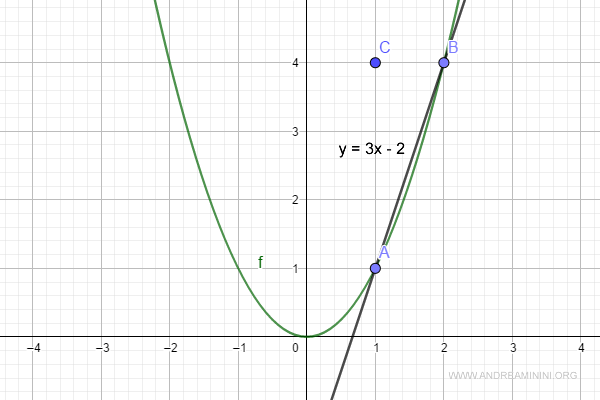
Si ahora evaluamos el límite del cociente incremental cuando h → 0:

$$ \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} = f'(x) $$

obtenemos la derivada f'(x).

Este valor representa también tan α, es decir, la pendiente de la tangente en A.

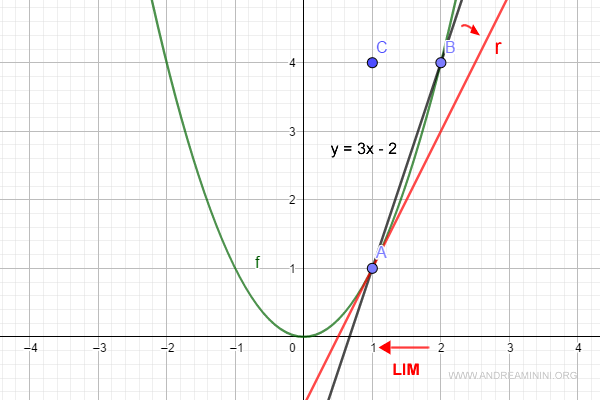
¿Cuál es la ecuación de la tangente?

En este caso nos interesa un único punto, no dos distintos.

Sabemos que el límite del cociente incremental equivale a tan α, que es la derivada f'(x):

$$ \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} = \tan \:\: \alpha = f'(x) $$

Por lo tanto, para hallar la pendiente de la tangente basta con conocer la derivada f'(x).

La derivada de f(x) = x² es:

$$ f'(x) = 2x $$

En x = 1 resulta:

$$ f'(1) = 2 $$

Así, la pendiente de la tangente en A es 2.

Determinamos su ecuación con la forma punto-pendiente:

$$ y - y_0 = m \cdot (x - x_0) $$

Con m = 2 y tomando A (1, 1):

$$ y - 1 = 2 \cdot (x - 1) $$

$$ y = 2x - 1 $$

De este modo hallamos la ecuación cartesiana de la tangente en A.

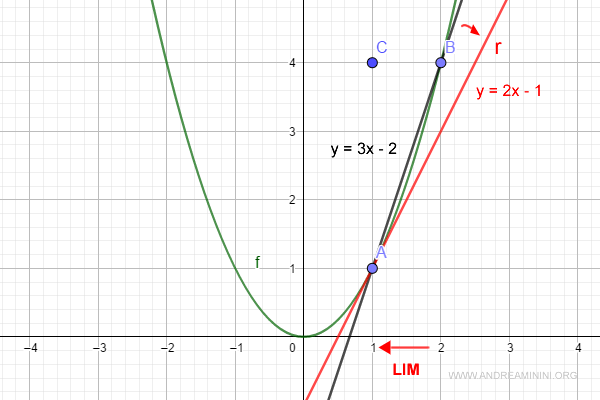
¿Cómo hallar la tangente en otro punto?

El procedimiento es el mismo:

Se calcula la pendiente de la tangente en el nuevo punto.

Y a continuación se construye su ecuación cartesiana usando las coordenadas de ese punto.

Ejemplo: la tangente en B

La recta r′ es tangente a la curva en B (en azul).

Su pendiente difiere de la de la tangente en A (en rojo), pues las inclinaciones no son iguales.

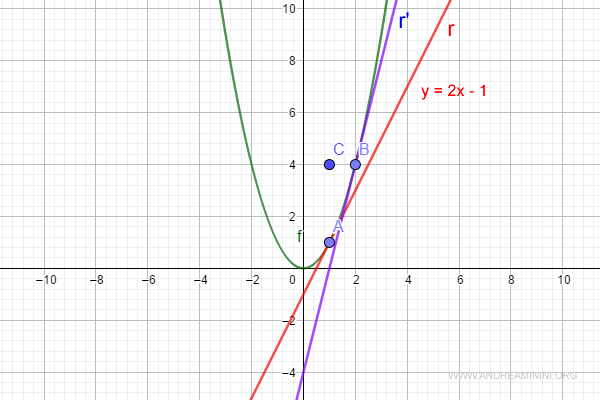
Aunque la derivada f'(x) es la misma función, la evaluamos ahora en x = 2.

La pendiente de r′ es 4:

$$ f'(x) = 2x = \tan \: \alpha $$

$$ f'(2) = 4 $$

Conocida la pendiente (m = 4), obtenemos la ecuación cartesiana de r′ con la misma fórmula:

$$ y - y_0 = m \cdot (x - x_0) $$

$$ y - y_0 = 4 \cdot (x - x_0) $$

Tomando B (2, 4) como referencia:

$$ y - 4 = 4 \cdot (x - 2) $$

$$ y = 4x - 4 $$

Así encontramos la ecuación de la tangente en B (en azul).

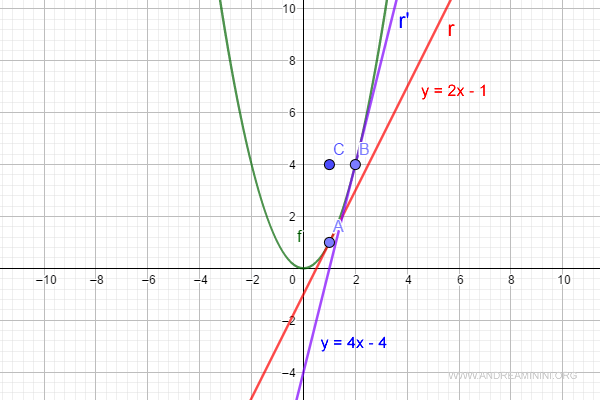
Y así sucesivamente.